
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài giải:
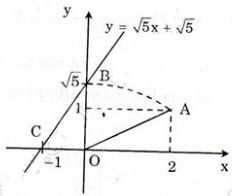
Hình bên diễn tả cách dựng đoạn thẳng có độ dài bằng √5.
Đồ thị hàm số y = √5 x + √5 đi qua hai điểm A(0; √5) và B(-1; 0).


Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)
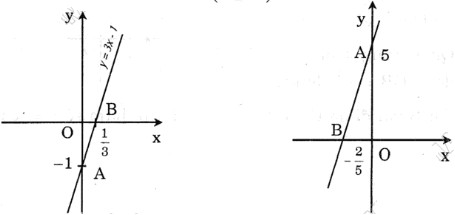

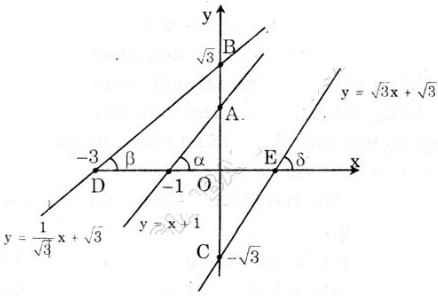
a) Đồ thị như hình bên.
b) tgα = 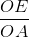 = 1,
= 1,
tgβ = 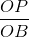 =
= 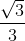 =
= 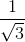 ,
,
tgɣ = 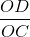 =
= 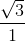 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .
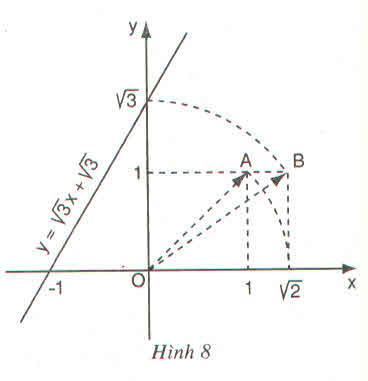
a) Đồ thị như hình bên.

b) tgα = 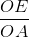 = 1,
= 1,
tgβ = 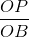 =
= 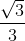 =
= 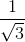 ,
,
tgɣ = 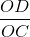 =
= 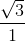 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .

\(y=\sqrt{x^2-2x+1}+\sqrt{x^2-6x+9}=\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-3\right)^2}\)
\(\Rightarrow y=\left|x-1\right|+\left|x-3\right|\)
- Xét \(x=0\Rightarrow y=\left|0-1\right|+\left|0-3\right|=\left|-1\right|+\left|-3\right|=4\)
- Xét \(y=0\Rightarrow\left|x-1\right|+\left|x-3\right|=0\Leftrightarrow\left|x-1\right|=\left|x-3\right|\)
\(\Rightarrow1\le x< 3\Leftrightarrow x-1=3-x\Leftrightarrow x=2\) (thỏa)
Vậy đồ thị hàm số đi qua \(A\left(0;4\right)\) và \(B\left(2;0\right)\)
---------------Tự vẽ nhé-------------------
mình biết nội quy rồi nên đưng đăng nội quy
ai chơi bang bang 2 kết bạn với mình
mình có nick có 54k vàng đang góp mua pika
ai kết bạn mình cho