K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Sách cũng có nói Parabol k thể được gọi là đồ thị hàm số. Mình hơi thắc mắc vì ở trường thầy cô đều nói là đồ thị hàm số bậc 1,2. Như vậy hàm số bậc 1,2 khi vẽ ra hệ descart có được gọi là đồ thị hs k ạ. Cao nhân giải đáp giúp mình với
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
Lý do gì em lại tin 1 cuốn sách có nguồn từ đâu đó hơn là tài liệu chính thống của BGD sử dụng trong đào tạo?
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2021
\(y=\dfrac{x+2}{x+1}\Rightarrow y'=\dfrac{-1}{\left(x+1\right)^2}\)
Gọi giao điểm của tiếp tuyến tại M với 2 trục lần lượt là A và B
Do tam giác OAB vuông cân \(\Rightarrow\widehat{ABO}=45^0\)
\(\Rightarrow\) Tiếp tuyến tạo với trục hoành một góc \(45^0\) hoặc \(135^0\)
\(\Rightarrow\) Hệ số góc k của tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}k=tan45^0=1\\k=tan135^0=-1\end{matrix}\right.\)
Gọi \(M\left(x_0;y_0\right)\) \(\Rightarrow y'\left(x_0\right)=k\Rightarrow\left[{}\begin{matrix}\dfrac{-1}{\left(x_0+1\right)^2}=1\left(vô-nghiệm\right)\\\dfrac{-1}{\left(x_0+1\right)^2}=-1\end{matrix}\right.\)
\(\Rightarrow\left(x_0+1\right)^2=1\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y_0=2\\x_0=-2\Rightarrow y_0=0\end{matrix}\right.\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(0;2\right)\\M\left(-2;0\right)\end{matrix}\right.\)
CM
21 tháng 8 2018
cos2(x + kπ) = cos(2x + k2π) = cos2x, k ∈ Z.
Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos2x
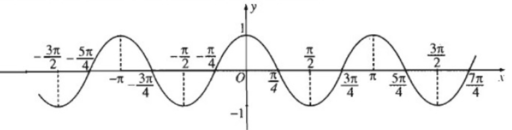
Đồ thị hàm số y = |cos2x|
PT
1
CM
25 tháng 2 2018
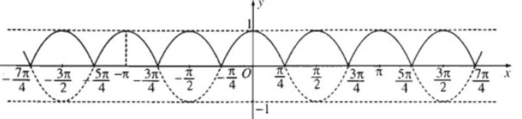
+ Đồ thị hàm số y = sin x.
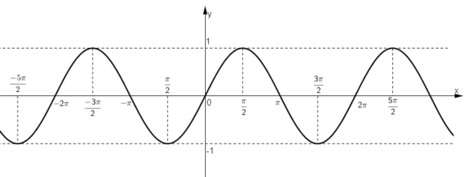
+ Ta có:
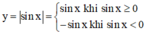
Vậy từ đồ thị hàm số y = sin x ta có thể suy ra đồ thị hàm số y = |sin x| bằng cách:
- Giữ nguyên phần đồ thị nằm phía trên trục hoành (sin x > 0).
- Lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.
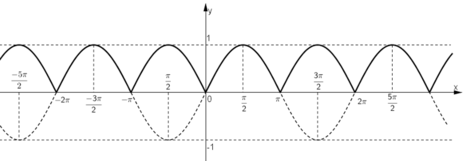
Ta được đồ thị hàm số y = |sin x| là phần nét liền hình phía dưới.
CM
26 tháng 3 2017
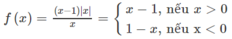
Hàm số này có tập xác định là R \ {0}
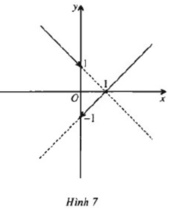
Từ đồ thị (H.7) dự đoán f(x) liên tục trên các khoảng (−∞;0), (0; +∞) nhưng không liên tục trên R. Thật vậy,
- Với x > 0, f(x) = x − 1 là hàm đa thức nên liên tục trên R do đó liên tục trên (0; +∞)
- Với x < 0, f(x) = 1 – x cũng là hàm đa thức nên liên tục trên R do đó liên tục trên (−∞; 0)
Dễ thấy hàm số gián đoạn tại x = 0 vì
12 tháng 9 2021
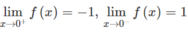
a, Lấy đối xứng tất cả các điểm trên đồ thị y = sinx (trừ gốc tọa độ) qua trục tung ta được đồ thị y = - sinx
b, Giữ nguyên phần đồ thị nằm bên trái Oy.
Bỏ phần đồ thị bên phải
Lấy đối xứng đồ thị nằm bên trái Oy qua Oy
Đồ thị y = sin|x| là hợp của 2 phần ở trên
c, Tịnh tiến độ thị y = sinx theo vecto \(\overrightarrow{u}=\left(1;0\right)\), hay nói dễ hiểu hơn là dịch chuyển đồ thị y = sinx lên trên 1 đơn vị độ dài
ta được đồ thị y = sinx + 1
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
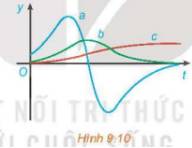
Hàm số c luôn đồng biến, tức là đạo hàm của nó phải luôn không âm, do đó hàm số b là đạo hàm của hàm số c; hàm số b đồng biến trên khoảng mà hàm số a dương và nghịch biến trên khoảng mà hàm số a âm, do đó hàm số a là đạo hàm của hàm số b.
Vậy hàm số a là hàm gia tốc, hàm số b là hàm vận tốc và hàm số c là hàm vị trí của ô tô.