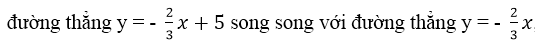Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
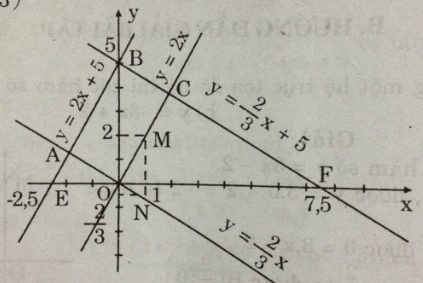
b)Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.
Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x, đường thẳng y = - 2x/3 +5 song song với đường thẳng y = - 2x/3 , tứ giác OABC là hình bình hành (có hai cặp cạnh song song).
Vậy tứ giác OABC là hình bình hành
a/ Bạn tự vẽ
b/ Ta lập pt hoành độ giao điểm :
(d1) giao với (d2) : \(-x-5=\frac{1}{4}x\Leftrightarrow x=-4\) thay vào (d1) được y = -1
Vậy A(-4;-1) . Tương tự ta tìm được điểm B(-1;-4)
c/ Ta có : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(-1+4\right)^2+\left(-4+1\right)^2}=3\sqrt{2}\)
\(OA=\sqrt{x_A^2+y_A^2}=\sqrt{4^2+1^2}=\sqrt{17}\) ; \(OB=\sqrt{x_B^2+y_B^2}=\sqrt{1^2+4^2}=\sqrt{17}\)
=> OAB là tam giác cân
d/ Gọi OH là đường cao hạ từ O xuống AB (H thuộc AB)
Vì tam giác OAB cân tại O nên AH = HB = 1/2AB = \(\frac{3\sqrt{2}}{2}\)
\(OH=\sqrt{OA^2-BH^2}=\sqrt{17-\left(\frac{3\sqrt{2}}{2}\right)^2}=\frac{5\sqrt{2}}{2}\)
\(S_{ABC}=\frac{1}{2}AB.OH=\frac{1}{2}.3\sqrt{2}.\frac{5\sqrt{2}}{2}=\frac{15}{2}\)
Bài giải:
a) Xem hình bên
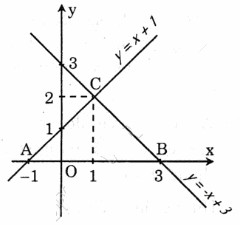
b) A(-1; 0), B(3; 0), C(1; 2).
c) Chu vi ∆ABC bằng 4(1 + √2).
Diện tích ∆ABC bằng 4cm2 .
theo hệ thức lượng thì OH x CD = Ox x Oy (C là giao điểm của d3 với Oy; D là giao điểm của d3 với Ox )
để OH max thì OH .CD max =>từ đây ko tính OH.CD vì nó max rồi
quay lại ta thấy OH.CD max <=> Ox x Oy bé hơn or bằng 0
mà Ox Oy của d3 thì theo hàm số d3 nhá
giải ra thì bạn dc :-(2m+6.5)2 - 52.25 bé hơn or bằn 0
=> m=-3.25
mình giải z dc ko bạn
bài tập hơi khó, 2 bài nên mấy bạn làm được bài nào cũng được ạ, e cảm ơn nhìu!!!