
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phần tử c và h không phải là chi tiết máy. Vì:
Phần tử h: Mảnh vỡ máy gồm nhiều phần chi tiết trong đó nên cũng không thể gọi là một chi tiết máy

Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

à cái bài hình chiếu là bài số 2 á, còn câu của mình hỏi thì để hiểu biêt thêm để làm bài thực hành thôi

Các quy ước vẽ hình chiếu:
- Chọn vị trí vật thể để vẽ hình chiếu từ trước ( Hình chiếu chính) sao cho thể hiện nhiều nhất và tương đối rõ ràng nhất những phần tử quan trọng của khối vật thể.
- Căn cứ vào mức độ phức tạp của khối vật thể mà chọn loại hình chiếu và số lượng hình chiếu cho đủ (không thừa, không thiếu)
- Nếu các vị trí các hình chiếu thay đổi vị trí thì phải ký hiệu bằng chữ.
Cách vẽ hình chiếu:
Bước 1: Quan sát vật thể, phân tích hình dạng và chọn hướng chiếu vuông góc với các bề mặt của vật thể để biểu diễn hình dạng vật thể.
Bước 2: Chọn tỉ lệ thích hợp với khổ giấy A4 và kích thước của vật thể. Bố trí ba hình chiếu cân đối trên bản vẽ theo các hình chữ nhật bao ngoài hình chiếu bằng nét liền mảnh.
Bước 3: Lần lượt vẽ bằng nét liền mảnh từng phần của vật thể với các đường gióng giữa các hình chiếu của từng phần.
Bước 4: Tô đậm các nét thấy, đường bao thấy của vật thể trên hình chiếu, dùng nét đứt biểu diễn các cạnh khuất, đường bao khuất.
Bước 5: Kẻ các đường gióng, đường ghi kích thước và con số kích thước trên các hình chiếu.
Bước 6: Kẻ khung bản vẽ, khung tên, ghi nội dung.
//mik chỉ bt đến đó thôi//
!!!Chúc bn hok tốt!!!

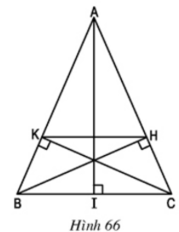
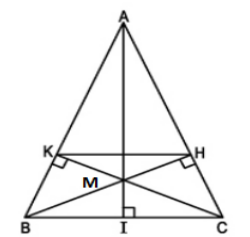
A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

A E B H D G F C
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF = AC/2.
HA = HD, HC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật
<=> EH ⊥ EF
<=>\(AC\perp BD\) (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
<=>EF = EH
<=> AC = BD (Vì \(EF=\frac{AC}{2},EH=\frac{BD}{2}\))
c) EFGH là hình vuông
<=> EFGH là hình thoi và EFGH là hình chữ nhật
<=> AC = BD và .\(AC\perp DB\)

Ta có: AB//CD(vì ABCD là hình thang)
=>góc ABD=góc CDB
Xét tam giác ABD và tam giác CDB:
AB=DC(GT)
Góc ABD=Góc CDB(cmt)
DB là cạnh chung
Vậy tam giác ABD=tam giác CDB(c.g.c)
=>AD=BC(2 cạnh tương ứng); góc ADB=góc CBD( 2 góc tương ứng)
Ta có: góc ABD=góc CBD(cmt)
Mà 2 góc này nằm ở vị trí so le trong nên AD//BC(theo tiên đề Ơ-clit)(đpcm)


bạn tra ở gg nhé