Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
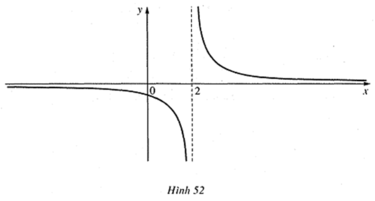
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị 0.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị 0.
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
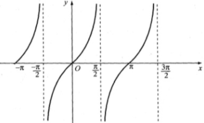
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
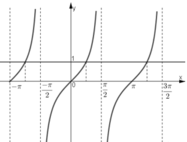
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
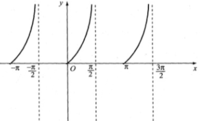
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
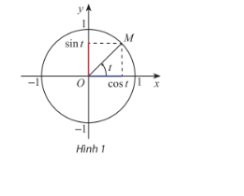
a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\) là hoành độ của điểm M trên đường tròn lượng giác.
Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất
Nên ta chỉ xác định duy nhất giá trị sint và cost.
b,
Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))
Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))
Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.
\(2x^2+3x-\left(m-1\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2>0\\\Delta=9+8\left(m-1\right)< 0\end{matrix}\right.\)
\(\Rightarrow m< -\dfrac{1}{8}\)
1, Phương trình tương đương
\(\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
⇔ \(sin\left(2x-\dfrac{\pi}{6}\right)=1\)
⇔ \(2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k.2\pi\)
⇔ x = \(\dfrac{\pi}{3}+k.\pi\)
2, \(2cos3x+3sin3x-2\)
= \(\sqrt{13}\)\((\dfrac{2}{\sqrt{13}}cos3x+\dfrac{3}{\sqrt{13}}sin3x)\) - 2
Do \(\left(\dfrac{2}{\sqrt{13}}\right)^2+\left(\dfrac{3}{\sqrt{13}}\right)^2=1\) nên tồn tại 1 góc a sao cho \(\left\{{}\begin{matrix}sina=\dfrac{2}{\sqrt{13}}\\cosa=\dfrac{2}{\sqrt{13}}\end{matrix}\right.\)
BT = \(\sqrt{13}sin\left(x+a\right)-2\)
Do - 1 ≤ sin (x + a) ≤ 1 với mọi x và a
⇒ \(-\sqrt{13}-2\le BT\le\sqrt{13}-2\)
⇒ \(-5,6< BT< 1,6\)
Vậy BT nhận 5 giá trị nguyên trong tập hợp S = {-5 ; -4 ; -3 ; -2 ; -1}
3. \(msinx-cosx=\sqrt{5}\)
⇔ \(\dfrac{m}{\sqrt{m^2+1}}.sinx-\dfrac{1}{\sqrt{m^2+1}}.cosx=\dfrac{\sqrt{5}}{\sqrt{m^2+1}}\)
⇔ sin(x - a) = \(\sqrt{\dfrac{5}{m^2+1}}\) với \(\left\{{}\begin{matrix}sina=\dfrac{1}{\sqrt{m^2+1}}\\cosa=\dfrac{m}{\sqrt{m^2+1}}\end{matrix}\right.\)
Điều kiện có nghiệm : \(\left|\sqrt{\dfrac{5}{m^2+1}}\right|\le1\)
⇔ m2 + 1 ≥ 5
⇔ m2 - 4 ≥ 0
⇔ \(\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Bài 1. a) trục hoành cắt đoạn đồ thị y = tanx (ứng với x ∈ .gif)
) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
b) Đường thẳng y = 1 cắt đoạn đồ thị y = tanx (ứng với x ∈ ) tại ba điểm có hoành độ .gif)
. Do đó trên đoạn chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là .gif)
.
c) Phần phía trên trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng .gif)
. Vậy trên đoạn , các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈ .png)
.
d) Phần phía dưới trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng .png)
. Vậy trên đoạn , các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈ .png)
.
a) \(\left\{-\pi;0;\pi\right\}\)
b) \(\left\{\dfrac{\pi}{4};\dfrac{\pi}{4}\pm\pi\right\}\)
c) \(\left(-\pi;-\dfrac{\pi}{2}\right)\cup\left(0;\dfrac{\pi}{2}\right)\cup\left(\pi;\dfrac{3\pi}{2}\right)\)
d) \(\left(-\dfrac{\pi}{2};0\right)\cup\left(\dfrac{\pi}{2};\pi\right)\)
sin2a cũng giống cos2a có thể có giá trị âm và dương và còn tùy thuộc góc 2a như thế nào? (Bạn có thể xem phần đường tròn lượng giác sẽ hiểu thêm điều này)