Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiếu lên trục tọa độ Ox có phương trùng với phương mp nghiêng, chiều hướng xuống
Oy có phương vuông góc với mpn, chiều hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:mg\sin\alpha\ge\mu N\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha\ge\mu mg\cos\alpha\)
\(\Leftrightarrow\sin\alpha\ge\mu\cos\alpha\)
Chỗ bạn học giải bpt lượng giác chưa vậy?

a) Khi vật nằm yên trên mặt phẳng nghiêng thì hợp lực tác dụng lên vật bằng không, ứng với góc α lớn nhất ta có:
mgsinα = μmgcosα tan α = μ = 0,45 và α ≈ 24 °.


Chọn B.
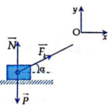
Áp dụng định luật II Niu-tơn:
![]()
Chiếu lên Oy: N = P – F.sinα
Chiếu lên Ox: F.cosα – μN = m.a
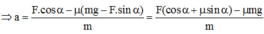
Theo Bất đẳng thức Bu-nhi-a - Cốp-xki:
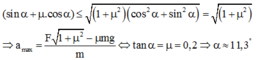

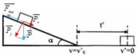
+ Gắn hệ trục tọa độ như hình vẽ
+ Viết phương trình định luật II – Niuton cho vật ta được:
P → + F m s → = m a → (1)
+ Chiếu (1) lên các phương ta được:
Ox:
P x − F m s = m a → a = P x − F m s m = P sin α − μ P cos α m = g sin α − μ g cos α
+ Vì mặt phẳng nghiêng nhẵn nên hệ số ma sát bằng 0, do đó: a = g . sin α = 10. sin 30 0 = 5 m / s 2
+ Vận tốc của vật ở cuối mặt phẳng nghiêng là: v = 2 a l = 2.5.10 = 10 m / s
+ Gia tốc của vật trên mặt phẳng ngang là:
a ' = − F m s m = − μ m g m = − μ g = − 0 , 1.10 = − 1 m / s 2
+ Thời gian vật đi trên mặt phẳng ngang là: t ' = v ' − v 0 ' a ' = 0 − v a ' (do vật dừng lại nên v′=0 )
Ta suy ra: t ' = − v a ' = − 10 − 1 = 10 s
Đáp án: B

Ta có P 1 x = P 1 . sin 30 0 = m 1 g . 1 2 = 0 , 8.10.0 , 5 = 4 ( N ) P 2 = m 2 g = 0 , 6.10 = 6 ( N )
Vậy P 2 > P 1 x vật hai đi xuống vật một đi lên, khi vật hai đi xuống được một đoạn s = 50 cm thì vật một lên cao
z 1 = s . sin 30 0 = s 2 = 25 ( c m )
Chọn vị trí ban đầu của hai vật là mốc thế năng
Theo định luật bảo toàn năng lượng
0 = W d + W t + A m s V ớ i W d = ( m 1 + m 2 ) v 2 2 = ( 0 , 8 + 0 , 6 ) .1 2 2 = 0 , 7 ( J ) A m s = F m s . s = μ m 1 g . cos 30 0 . s = μ .0 , 8.10. 3 2 .0 , 5 = μ 2 3 ( J )
Vậy 0 = 0 , 7 − 1 + μ .2. 3 ⇒ μ = 0 , 0866
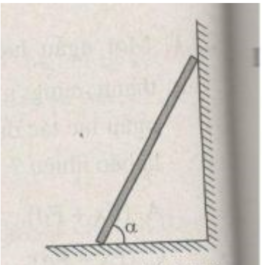
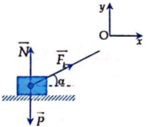
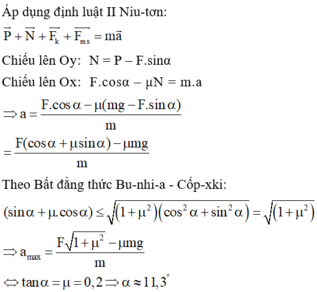
Để xe nằm yên ko trượt đồng nghĩa với việc các lực t/d lên nó phải triệt tiêu nhau, nghĩa là: \(\overrightarrow{P}+\overrightarrow{F_{ms}}+\overrightarrow{N}=\overrightarrow{0}\)
\(\Rightarrow\left\{{}\begin{matrix}mg\sin\alpha=\mu N\\N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha=\mu mg\cos\alpha\)
\(\Leftrightarrow\sin\alpha=0,2\cos\alpha\)
Thấy cos alpha=0 ko là nghiệm của phương trình, chia 2 vế cho cos alpha \(\tan\alpha=0,2\Rightarrow\alpha=11^0\)