Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tìm tần số dao động của con lắc, ta có công thức:
f = 1/T
Trong đó: f là tần số dao động (Hz) T là chu kì dao động (s)
Theo đề bài, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s là T/3. Độ lớn gia tốc của con lắc được tính bằng công thức:
a = -ω²x
Trong đó: a là gia tốc (cm/s²) ω là góc tốc độ góc của con lắc (rad/s) x là biên độ dao động (cm)
Ta có thể tính được ω bằng công thức:
ω = 2πf
Thay vào công thức gia tốc, ta có:
a = -(2πf)²x = -4π²f²x
Đề bài cho biết gia tốc không vượt quá 100 cm/s, nên ta có:
100 ≥ 4π²f²x
Với x = 5 cm, ta có:
100 ≥ 4π²f²(5)
Simplifying the equation:
5 ≥ π²f²
Từ đó ta có:
f² ≤ 5/π²
f ≤ √(5/π²)
f ≤ √(5/π²) ≈ 0.798 Hz
Vậy tần số dao động của con lắc là khoảng 0.798 Hz.

Áp dụng: \(v_{max}= \omega A \Rightarrow \omega = \frac{v_{max}}{A} = \frac{10\pi}{5} = 2\pi \ (rad/s)\)
\(\Rightarrow T = \frac{2\pi}{\omega} = 1 s\)

Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Theo đề bài ta có
![]()
![]()
Biểu diễn trên đường tròn lượng giác ta có :
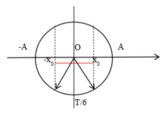
Từ đường tròn lượng giác ta thấy phần gạch đỏ là phần thỏa mãn yên cầu của đề bài => x0 = A/2 = 2,5 cm
Do đó ta có :
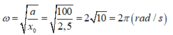
=> Tần số f = ω / 2 π => Chọn A






Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)