Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông tại B có \(tanC=\dfrac{AB}{BC}\)
=>\(AB=BC\cdot tanC=12\cdot tan35\simeq8,4\left(m\right)\)

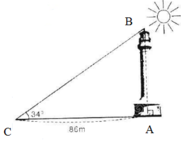
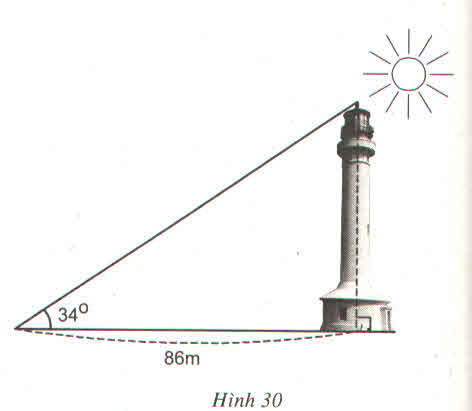
Kí hiệu đỉnh như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:
A B = A C . t g 34 ° = 86 . t g 34 ° ≈ 58 ( m )
Vậy chiều cao tòa nhà là 58m.

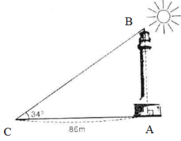
Kí hiệu đỉnh như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:
AB = AC.tg34o = 86.tg34o ≈ 58 (m)
Vậy chiều cao tòa nhà là 58m.

\(tanC=\dfrac{AB}{AC}\Rightarrow AB=AC\cdot tanC=100\cdot tan40^0\approx84m\)
Chọn A

Xét \(\Delta\) ABC vuông tại A
\(\tan\left(\widehat{C}\right)=\dfrac{AB}{AC}\)
\(\Leftrightarrow tan\left(34^0\right)=\dfrac{AB}{89}\)
\(\Leftrightarrow AB=60,03m\)

Gọi tam giác ABC vuông tại A với AC là bóng của cột cờ trên mặt đất
Áp dụng tslg của góc nhọn trong tam giác ABC vuông tại A:
\(tanC=\dfrac{AB}{AC}\)
\(\Rightarrow tan50^0=\dfrac{AB}{22}\Rightarrow AB=tan50^0.22\simeq26\left(m\right)\)
Vậy chiều dài cột cờ khoảng 26m

Chiều cao của tháp là: \(24.tan32^0\approx15\left(m\right)\)

Gọi a là chiều cao của tháp, ta có:
\(\tan34\) = \(\dfrac{c.đối}{c.kề}\)= \(\dfrac{a}{86}\)
\(\Rightarrow a=\) \(\tan34.86\) \(\approx\) 58m
Vậy chiều cao của tháp là 58m
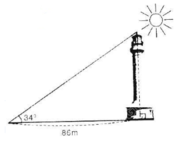
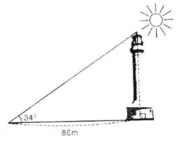

AB là chiều cao của tượng đài, góc C là góc tạo bởi tượng đài và mặt đất
Ta có:
\(tanC=\dfrac{AB}{BC}\)
\(\Rightarrow tan30^o=\dfrac{AB}{17,32}\)
\(\Rightarrow AB=17,32\cdot tan30^o\approx10\left(m\right)\)
Vậy: ...