Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành

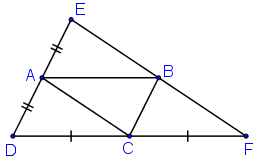
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B

Ta có: AE+EB=AB
CF+FD=CD
mà AB=CD
và AE=CF
nên EB=FD
Ta có: AH+HD=AD
CG+BG=CB
mà AD=CB
và HD=BG
nên AH=CG
Xét ΔAHE và ΔCGF có
AH=CG
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔAHE=ΔCGF
Suy ra: HE=GF
Xét ΔEBG và ΔFDH có
EB=FD
\(\widehat{B}=\widehat{D}\)
BG=DH
Do đó: ΔEBG=ΔFDH
Suy ra: EG=FH
Xét tứ giác EHFG có
EG=FH
EH=FG
Do đó: EHFG là hình bình hành

Câu thứ nhất sai đề bạn ạ vì ko có tia đối của tia AD