Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A’B’=2,2 cm
A’C’=3,4 cm
Hai tam giác \(ABC\) và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.

a) Xét △���△ABC có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác △���△BEA và △���△BEH.
có ��BE là cạnh chung
���^=���^(=90∘)��=�� suy ra △���=△��� (c.h-cgv) ⇒���^=���^ suy ⇒BAE=BHE(=90
a) Xét △���△ABC có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác △���△BEA và △���△BEH.
có ��BE là cạnh chung
���^=���^(=90∘)��=�� suy ra △���=△��� (c.h-cgv) ⇒���^=���^ suy ⇒BAE=BHE(=90


b) Vì \(AH\perp BC\left(gt\right)\)
=> \(AH\perp BB'.\)
=> \(AH\) là đường trung trực của \(BB'.\)
Mà \(A\in\) đường trung trực của \(BB'.\)
=> \(AB=AB'\) (định lí đường trung trực).
=> \(\Delta ABB'\) cân tại A.
Chúc bạn học tốt!


Dịch: Tìm số nguyên tố p sao cho tồn tại số nguyên dương a; b sao cho \(\frac{1}{p}=\frac{1}{a^2}+\frac{1}{b^2}\)
Vì \(\frac{1}{p}=\frac{1}{a^2}+\frac{1}{b^2}\) => (a2 + b2).p = a2.b2 (*) => a2b2 chia hết cho p => a2 chia hết cho p hoặc b2 chia hết cho p
+) Nếu a2 chia hết cho p ; p là số nguyên tố => a chia hết cho p => a2 chia hết cho p2 => a2 = k.p2 ( k nguyên dương)
Thay vào (*) ta được (a2 + b2) . p = k.p2.b2 => a2 + b2 = kp.b2 => a2 + b2 chia hết cho p => b2 chia hết cho p
=> b chia hết cho p
+) Khi đó, đặt a = m.p; b = n.p . thay vào \(\frac{1}{p}=\frac{1}{a^2}+\frac{1}{b^2}\) ta được: \(\frac{1}{p}=\frac{1}{m^2p^2}+\frac{1}{n^2p^2}\)
=> \(\frac{1}{p}=\frac{1}{p^2}\left(\frac{1}{m^2}+\frac{1}{n^2}\right)\)=> \(\frac{1}{m^2}+\frac{1}{n^2}=p\)
+) Vì p là số nguyên tố nên p > 2 . mà a; b nguyên dương nên m; n nguyên dương => m; n > 1 => \(\frac{1}{m^2}+\frac{1}{n^2}\le1+1=2\)
=> p = 2 và \(\frac{1}{m^2}+\frac{1}{n^2}=2\) => m = n = 1
Vậy p = 2 và a = b = 2

a) Chứng minh rằng nếu hai góc xOyxOy và x′O′y′x′O′y′ cùng nhọn có Ox⊥O′x′Ox⊥O′x′,Oy⊥O′y′Oy⊥O′y′ thì ˆxOy=ˆx′O′y′

Tham khảo
length = 19 feets and breadth = 18 feets
Given, area of the dining room = 342 square feet.
We know that, area of rectangle = length x breadth
Implies, the length and breadth are the factors of 342
Prime factorisation of 342 = 2 x 3 x 3 x 19
Given that the approximate length of one side is a prime number less than 25.
The nearest prime number less than 25 and a factor of 342 is 19.
Therefore, the approximate length of the room = 19 feet
Hence, breadth =\(\dfrac{area}{length}\)=\(\dfrac{342}{19}\)=18 feet
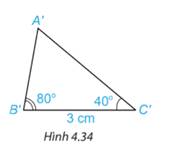
Các góc tương ứng của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.