K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
FF
3
25 tháng 2 2019
Bài làm
~ Mình có được không ~
# Chúc bạn học tốt #
TP
0
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 5 2021
1.
\(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều
\(\Rightarrow S_{ABCD}=2S_{ABC}=2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{2}\)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow SO\perp AC\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{AC\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{a^3}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 5 2021
2.
Gọi M là trung điểm AB \(\Rightarrow SM\perp AB\Rightarrow SM\perp\left(ABCD\right)\)
\(SM=\dfrac{AB\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam giác vuông MBC:
\(CM^2=BM^2+BC^2=\left(\dfrac{AB}{2}\right)^2+\left(2AB\right)^2=\dfrac{17AB^2}{4}\)
Áp dụng định lý Pitago cho tam giác vuông SMC:
\(SC^2=SM^2+CM^2\Leftrightarrow5a^2=\dfrac{3AB^2}{4}+\dfrac{17AB^2}{4}=5AB^2\)
\(\Rightarrow AB=a\Rightarrow\left\{{}\begin{matrix}AD=2a\\SM=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
\(V=\dfrac{1}{3}.SM.AB.AD=\dfrac{a^3\sqrt{3}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2019
Làm biếng vẽ hình quá, bạn tự vẽ :D
1/ Dễ dàng nhận ra các tam giác BAD và BCD đều
Do \(AB//\left(SCD\right)\Rightarrow d\left(B;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Từ A kẻ \(AH\perp CD\Rightarrow AH=\frac{a\sqrt{3}}{2}\Rightarrow CD\perp\left(SAH\right)\)
Từ A kẻ \(AK\perp SH\Rightarrow AK\perp\left(SCD\right)\)
\(\Rightarrow AK=d\left(A;\left(SCD\right)\right)=d\left(B;\left(SCD\right)\right)\)
Áp dụng hệ thức lượng: \(\frac{1}{AK^2}=\frac{1}{AH^2}+\frac{1}{SA^2}\Rightarrow AK=\frac{SA.AH}{\sqrt{SA^2+AH^2}}=...\)
Câu 2:
OA cắt \(\left(SBC\right)\) tại C, mà O là trung điểm AC
\(\Rightarrow d\left(O;\left(SBC\right)\right)=\frac{1}{2}d\left(A;\left(SBC\right)\right)\)
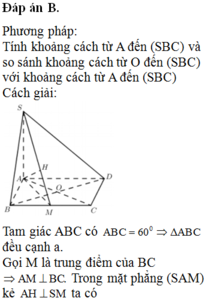
Tương tự như câu trên, tam giác ABC đều, từ A kẻ \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\)
\(\Rightarrow AH=\frac{a\sqrt{3}}{2}\)
Từ A kẻ \(AK\perp SH\Rightarrow AK\perp\left(SBC\right)\)
\(\Rightarrow AK=d\left(A;\left(SBC\right)\right)=2d\left(O;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng:
\(\frac{1}{AK^2}=\frac{1}{AH^2}+\frac{1}{SA^2}\Rightarrow d\left(O;\left(SBC\right)\right)=\frac{1}{2}AK=\frac{SA.AH}{2\sqrt{SA^2+AH^2}}=...\)
/?
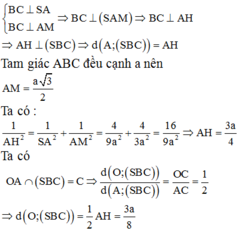
ụa j z