Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
\(s_1+s_2=\dfrac{v_1^2}{2a_1}+\dfrac{-v_1^2}{2a_2}=\dfrac{v_1^2}{2\cdot2}+\dfrac{-v_1^2}{2\cdot\left(-2,5\right)}=180\Rightarrow v_1=20\left(\dfrac{m}{s}\right)\)
Quãng đường chuyển động của xe trong từng giai đoạn
\(s_1=\dfrac{v_1^2}{2\cdot a_1}=\dfrac{20^2}{2\cdot2}=100\left(m\right);s_2=\dfrac{-v_1^2}{2\cdot a_2}=-\dfrac{20^2}{2\cdot\left(-2,5\right)}=80\left(m\right)\)
Thời gian qua từng giai đoạn
\(t_1=\sqrt{\dfrac{2s_1}{a_1}}=10\left(s\right);t_2=\sqrt{\dfrac{2s_2}{a_2}}=8\left(s\right)\)

a) Chọn Ox có gốc tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc hai xe bắt đầu chuyển động. Suy ra x 01 = 0; x 02 = 300 m.
- Với xe thứ nhất chuyển động theo chiều dương của Ox nên: v 01 = 10m/s và chuyển động nhanh dần đều nên a 1 = 2 m/ s 2 (do v 01 a 1 > 0) (0,25đ)
- Xe thứ hai chuyển động theo chiều âm của Ox nên v 02 = - 20 m/s và chuyển động chậm dần đều nên a 2 = 2 m/ s 2 (do v 02 a 2 < 0), x 2 = 300 m. (0,25đ)
Phương trình chuyển động của xe thứ nhất:
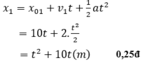
Phương trình chuyển động của xe thứ hai:
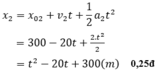
b) Khoảng cách giữa hai xe:
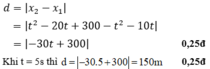
c) Hai xe gặp nhau khi: 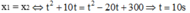 (0,25đ)
(0,25đ)
Vậy hai xe gặp nhau sau 10s.
Khi đó thay t = 10s vào ta có: 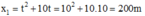 (0,25đ)
(0,25đ)
Suy ra vị trí gặp nhau cách vị trí xuất phát ban đầu của xe thứ 1 là 200 m.

Tại vị trí gặp nhau của hai xe thì
Xe xuất phát từ A có vận tốc bằng
v 1 = a 1 t = 2,5. 10 - 2 .400 = 10(m/s) = 36(km/h)
Xe xuất phát từ B có vận tốc bằng
v 2 = a 2 t = 2,0. 10 - 2 .400 = 8(m/s) = 28,8(km/h)

Khi hai xe máy gặp nhau thì x 1 = x 2 , nghĩa là:
1,25. 10 - 2 t 2 = 400 + 1,0. 10 - 2 t 2 hay ⇒ t = 400 s
Như vậy sau thời gian t = 400 s = 6 phút 40 giây kể từ lúc xuất phát thì hai xe đuổi kịp nhau.
Thay vào ta tìm được vị trí hai xe đuổi kịp nhau cách A đoạn x1 = 1,25. 10 - 2 . 400 2 = 2000 m = 2 km

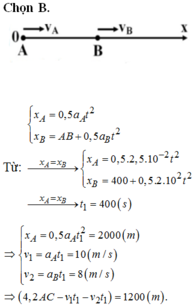
Vì gia tốc của NDĐ và CDĐ bằng nhau và bằng 0,4m/s² nên thời gian tăng tốc và giảm tốc là bằng nhau và quãng đường tăng tốc và giảm tốc cũng bằng nhau và bằng 90/2=45m
Ta có thời gian tăng tốc là:
\(s=\frac{1}{2}at^2\rightarrow t=\sqrt{\frac{2s}{a}}=\sqrt{\frac{2.45}{0,4}}=15s\)
Thời gian từ lúc xuất phát đến khi dừng lại trước mặt anh CSGT là 2t=30s