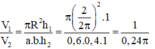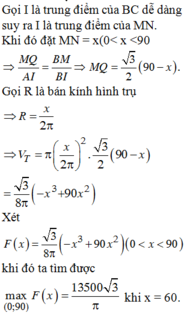Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Phương pháp: Sử dụng công thức thể tích hình trụ và công thức thể tích hình hộp.
Cách giải:
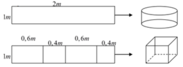
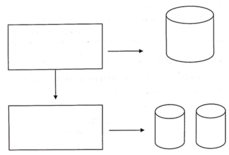
Ban đầu bán kính đáy là R, sau khi cắt và gò ta được 2 khối trụ có bán kính đáy là R 2 . Đường cao của các khối trụ không thay đổi. Ta có:
V 1 = S d h = π . R 2 . h V 2 = 2 S dl . h = 2 π R 2 h = πR 2 h 2
Khi đó: V 1 V 2 = 2
Đáp án C
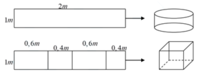
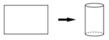
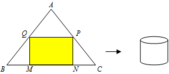
Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
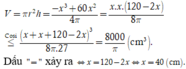
Chọn C.
Ta có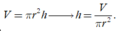 
Gọi t là giá tiền của một đơn vị diện tích vật liệu để làm mặt xung quanh, suy ra giá tiền của một đơn vị diện tích vật liệu để làm mặt đáy là 3t
Diện tích mặt xung quanh 
giá tiền mặt xung quanh là 
Diện tích hai mặt đáy 
giá tiền hai mặt đáy là 
Tổng tiền hoàn thành sản phẩm:
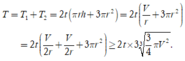
Dấu "=" xảy ra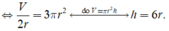 
Chọn C.
Đáp án C
Phương pháp: Lập hàm số chi phí theo một ẩn sau đó tìm giá trị nhỏ nhất của hàm số đó.
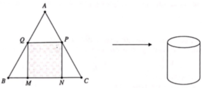
Cách giải: Gọi a là chiều dài cạnh đáy hình vuông của hình hộp chữ nhật và b là chiều cao của hình hộp chữ nhật ta có a 2 b = 8 a , b > 0 ⇒ a b = 8 a
Diện tích đáy hình hộp là a 2 và diện tích xung quanh là 4ab nên chi phí để làm thùng tôn là 100 a 2 + 50.4 a b = 100 a 2 + 200 a b = 100 a 2 = 100. 8 a = 100 a 2 + 1600 a = 100 a 2 + 16 a
Áp dụng BĐT Cauchy ta có a 2 + 16 a = a 2 + 8 a + 8 a ≥ 3 a 2 + 8 a + 8 a 3 = 3.4 = 12
Dấu bằng xảy ra khi và chỉ khi a 2 + 8 a ⇔ a = 2.
Vậy chi phí nhỏ nhất bằng 1200000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.
