

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Hướng dẫn làm bài:

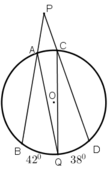
Ta có ˆBPDBPD^ là góc ở ngoài đường tròn (O) nên:
ˆBPD=sđcungBQD−sđcungAC2BPD^=sđcungBQD−sđcungAC2
Ta có ˆAQCAQC^ là góc nội tiếp trong đường tròn (O) nên:
ˆAQC=12sđcungACAQC^=12sđcungAC
Do đó:
ˆBPD+ˆAQC=sđcungBQF−sđcungAC2+sđcungAC2=sđcungBQD2=420+3802=400BPD^+AQC^=sđcungBQF−sđcungAC2+sđcungAC2=sđcungBQD2=420+3802=400
Vậy ˆBPD+ˆAQC=400

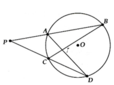
a, Ta có: B P D ^ = 1 2 s đ B D ⏜ - s đ A C ⏜ , A Q C ^ = 1 2 s đ B D ⏜ + s đ A C ⏜
=> B P D ^ + A Q C ^ = s đ B D ⏜ = 140 0
=> B C D ^ = 70 0
b, HS tự chứng minh

O C F A E B M P Q 1
+) Bước 1: Chứng minh \(\Delta\) FPO vuông tại P
Ta có: \(\widehat{O_1}=\widehat{FOP}=\widehat{FOE}=\widehat{FOM}+\widehat{MOE}=\frac{1}{2}\widehat{COM}+\frac{1}{2}\widehat{MOB}=\frac{1}{2}\widehat{BOC}\)
=> \(\widehat{FOP}=\frac{1}{2}\widehat{BOC}\)
mà \(\widehat{FCP}=\widehat{FCB}=\frac{1}{2}\widehat{BOC}\) ( góc nội tiếp = 1/2 góc ở tâm khi chắn cùng một cung)
=> \(\widehat{FOP}=\widehat{FCP}\)
=> Tứ giác CFPO nội tiếp => \(\widehat{FPO}+\widehat{FCO}=180^o\Rightarrow\widehat{FPO}=180^o-90^o=90^o\)
=> \(\Delta\) FPO vuông tại P
+) Bước 2: Chứng minh \(\Delta\) EQO vuông tại Q. ( Chứng minh tương tự)
+) Bước 3: Chứng minh tỉ số: \(\frac{PQ}{EF}=\frac{OQ}{OE}\)
Xét \(\Delta\) FPO vuông tại P và \(\Delta\) EQO vuông tại Q có: \(\widehat{O_1}\) chung
=> \(\Delta\) FPO ~ \(\Delta\) EQO
=> \(\frac{OQ}{OE}=\frac{OP}{OF}\)
Xét \(\Delta\) OQP và \(\Delta\) OEF có: \(\frac{OQ}{OE}=\frac{OP}{OF}\)( chứng minh trên ) và \(\widehat{O_1}\) chung
=> \(\Delta\) OQP ~ \(\Delta\) OEF
=> \(\frac{PQ}{EF}=\frac{OQ}{OE}\)(1)
+) Bước 4: Chứng minh Tỉ số \(\frac{PQ}{EF}\)không đổi khi M di chuyển trên cung nhỏ BC
Xét \(\Delta\)EQO vuông tại Q => \(\cos\widehat{O_1}=\frac{OQ}{OE}\)
Mặt khác : \(\widehat{O_1}=\frac{1}{2}\widehat{BOC}\) ( xem chứng minh ở Bước 1)
=> \(\cos\frac{1}{2}.\widehat{BOC}=\frac{OQ}{OE}\) (2)
Từ (1) ; (2) => \(\frac{PQ}{EF}=\cos\frac{1}{2}.\widehat{BOC}\)không đổi khi M di chuyển. ::))