Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc toạ độ O ở đỉnh tháp, trục toạ độ ox theo hướng v0 trục oy thẳng đứng xuống dưới.
Gốc thời gian là lúc ném vật.
Theo phương ox: Vật chuyển động thẳng đều với vận tốc vx = v0; x0 = 0
Theo phương oy: vật chuyển động nhanh dần đều với vận tốc đầu v0y = 0 ; y0 = 0
a. Phương trình toạ độ của quả cầu:
=> x = v0t => x = 20t (a)
=> y = 1/2 gt2 => y = 5t2 (b)
Lúc t = 2s => x = 40m => y = 60m
b. Phương trình quỹ đạo của quả cầu:
Từ (a) => t = x/20 thế vào (b) ta có :
\(y=5\left(\frac{x}{20}\right)^2=\frac{1}{80}x^2\left(m\right)\) (\(x\ge0\))
=> Quỹ đạo là đường Parabol, đỉnh O
c.Khi quả cầu chạm đất thì y = 80 m
Ta có y = 1/80 x2 = 80 => x = 80 m
Quả cầu chạm đất tại nơi cách chân tháp 80 m
Vận tốc quả cầu: \(v=\sqrt{v^2_x+v_y^2}=\sqrt{v_0^2+\left(gt\right)^2}\)
Thời gian để quả cầu chạm đất
\(t=\frac{2y}{9}=4s\)
Vậy : v = \(\sqrt{20^2+\left(10.4\right)^2}\approx44,7\) m/s

Chọn đáp án A
+ Chọn gốc tọa độ O ở đỉnh tháp, trục tọa độ Ox theo hướng v 0 → , trục OY thẳng đứng hướng xuống, gốc thời gian là lúc vừa ném vật.
+ Phương trình tọa độ của quả cầu:
x = v 0 t y = 1 2 g t 2 ⇒ x = 20 t m y = 5 t 2
Lúc t=2s: x = 40 m y = 20 m


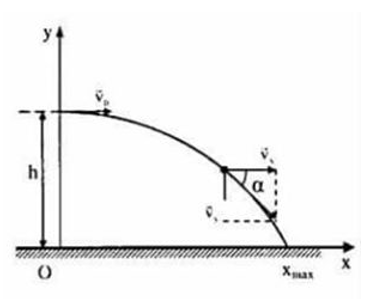
Chọn gốc tọa độ tại mặt đất.
\(v_0\) là vận tốc ban đầu vật.
\(Ox:\left\{{}\begin{matrix}v_x=v_0=hằngsố\\x=v_0\cdot t\end{matrix}\right.\)
\(Oy:\left\{{}\begin{matrix}v_y=g\cdot t\\y=h-\dfrac{1}{2}gt^2\end{matrix}\right.\)
Tại thời điểm \(t=4a;\alpha=30^o\)\(\Rightarrow v_x=v_y\)
\(\Rightarrow v_0=g\cdot t=10\cdot4=40\)m/s
Thời gian vật chạm đất\(\left(y=0\right)\)
\(\Rightarrow h-\dfrac{1}{2}gt^2=0\Rightarrow h=\dfrac{1}{2}gt^2\)
\(\Rightarrow t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot180}{10}}=6s\)
Phương trình quỹ đạo của quả cầu:
\(y=\dfrac{g}{2v_0^2}\cdot x^2=\dfrac{10}{2\cdot40^2}\cdot x^2=\dfrac{x^2}{320}\)
Vận tốc khi chạm đất:
\(v=\sqrt{v^2_0+\left(g\cdot t\right)^2}=\sqrt{40^2+\left(10\cdot4\right)^2}=40\sqrt{2}\)m/s
Khi đó góc tính đc:
\(v^2=v^2_0+\left(g\cdot t\right)^2=\left(v_0\cdot cos\beta\right)^2\)
\(\Rightarrow v=v_0\cdot cos\beta\Rightarrow cos\beta=\dfrac{v}{v_0}=\dfrac{40\sqrt{2}}{40}=\sqrt{2}\)
Hơi vô lí

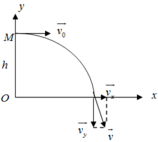
a. Chọn hệ quy chiếu Oxy với O là ở mặt đất
+ Trên trục Ox ta có :
a x = 0 ; v x = v o ; x = v o t
+ Trên trục Oy ta có :
a y = - g ; v y = - g t = - 10 t
y = h − 1 2 g t 2 = 80 − 5 t 2
Khi vận tốc của vật hợp với phương thẳng đứng một góc 45 0
Ta có tan 45 0 = v x v y = v 0 10 t ⇒ v 0 = 10 t = 10.3 = 30 m / s
b. Chạm đất: y = 0 ⇒ 5 t 2 = 80 ⇒ t = 4 s
Khi đó : x max = v 0 t = 30.4 = 120 m ; v y = g t = 10.4 = 40 m / s
⇒ v = v y 2 + v x 2 = 40 2 + 30 2 = 50 m / s

a) Phương trình tọa độ : \(\left\{{}\begin{matrix}x=v_0t=20t\\y=\dfrac{1}{2}gt^2=5t^2\end{matrix}\right.\)
b) Phương trình quỹ đạo : \(x=20t\rightarrow t=\dfrac{x}{20}\rightarrow y=\dfrac{1}{2\cdot20^2}\cdot10\cdot x^2=\dfrac{x^2}{80}\)
c) Tầm xa \(L=v_0\sqrt{\dfrac{2h}{g}}=20\sqrt{\dfrac{2\cdot80}{10}}=80\left(m\right)\)
Vận tốc khi chạm đất: \(v=\sqrt{v_0^2+2hg}=\sqrt{20^2+2\cdot80\cdot10}=44,7\left(m/s\right)\)

Chọn hệ quy chiếu với gốc tọa độ là vị trí ban đầu, trục Oy hướng xuống dưới, trục Ox trùng hướng với vecto vận tốc ban đầu. Gốc thời gian tại lúc ném
Thời gian quả cầu rơi là:
$t = \sqrt{\dfrac{2H}{g}} = \sqrt{\dfrac{2.80}{10}} = 4 (s)$
Vận tốc của quả cầu lúc chạm đất là:
$v = \sqrt{v_0^2 + 2gH} = \sqrt{20^2 + 2.10.80} = 20\sqrt{5} (m/s)$.