Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc MAO+góc MBO=90+90=180 độ
=>MAOB nội tiếp
ΔOCD cân tại O
mà OK là trung tuýen
nên OK vuông góc CD
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
góc OHE+góc OKE=90+90=180 độ
=>OHEK nội tiếp
b: Xét ΔMAE và ΔMKA có
góc MAE=góc MKA
góc AME chung
=>ΔMAE đồng dạng với ΔMKA
=>MA/MK=ME/MA
=>MA^2=MK*ME=MC*MD
1: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB và MO là phân giác của góc AMB
Ta có: MA=MB
=>M nằm trên đường trung trực của AB (2)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(1)
Từ (1),(2) suy ra OM là đường trung trực của AB
=>OM⊥AB tại H và H là trung điểm của AB
Xét (O) có
\(\hat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC
\(\hat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\hat{MAC}=\hat{ADC}\)
Xét ΔMAC và ΔMDA có
\(\hat{MAC}=\hat{MDA}\)
góc AMC chung
Do đó: ΔMAC~ΔMDA
=>\(\frac{MA}{MD}=\frac{MC}{MA}\)
=>\(MA^2=MD\cdot MC\left(3\right)\)
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(4\right)\)
Từ (3),(4) suy ra \(MD\cdot MC=MH\cdot MO\)
=>\(\frac{MD}{MO}=\frac{MH}{MC}\)
=>\(\frac{MD}{MH}=\frac{MO}{MC}\)
Xét ΔMDO và ΔMHC có
\(\frac{MD}{MH}=\frac{MO}{MC}\)
góc DMO chung
Do đó: ΔMDO~ΔMHC
=>\(\hat{MDO}=\hat{MHC}\)
mà \(\hat{MHC}+\hat{OHC}=180^0\) (hai góc kề bù)
nên \(\hat{OHC}+\hat{ODC}=180^0\)
=>OHCD là tứ giác nội tiếp
=>\(\hat{DHO}=\hat{DCO}\)
mà \(\hat{DCO}=\hat{ODC}\) (ΔOCD cân tại O)
và \(\hat{ODC}=\hat{MHC}\)
nên \(\hat{MHC}=\hat{OHD}\)
=>\(90^0-\hat{MHC}=90^0-\hat{OHD}\)
=>\(\hat{CHA}=\hat{DHA}\)
=>HA là phân giác của góc DHC
mà HA⊥HM
nên HM là phân giác ngoài tại đỉnh H của ΔDHC
Xét ΔDHC có HM là phân giác ngoài tại đỉnh H
nên \(\frac{MC}{MD}=\frac{HC}{HD}\)
2: Ta có: \(\hat{HAP}+\hat{OPA}=90^0\) (ΔAHP vuông tại H)
\(\hat{MAP}+\hat{OAP}=\hat{OAM}=90^0\)
mà \(\hat{OAP}=\hat{OPA}\) (ΔOAP cân tại O)
nên \(\hat{HAP}=\hat{MAP}\)
=>AP là phân giác của góc HAM
Xét ΔBAM có
AP,MH là các đường phân giác
AP cắt MH tại P
Do đó: P là tâm đường tròn nội tiếp ΔMAB
Tr oii câu này ra lâu lắm rồi mà chả có ai trả lời. Chắc bây giờ bn í tầm 17 tuổi r ^_^
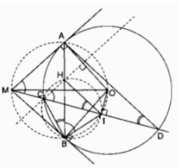
A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
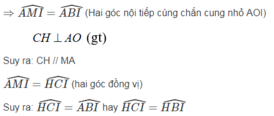
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.
