Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
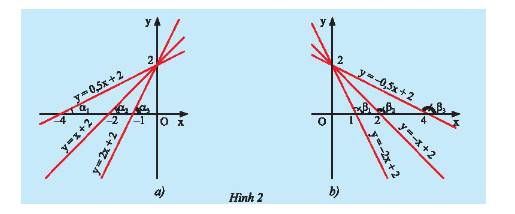
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).

a)
- Ở hình 1a là đồ thị của hàm số \(y = 0,5x + 2\) hệ số \(a = 0,5 > 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc nhọn.
- Ở hình 1b là đồ thị của hàm số \(y = - 0,5x + 2\) hệ số \(a = - 0,5 < 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc tù.

a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).
Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).
Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.
Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.
b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).
Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:
\(2 = 1.a'' \Rightarrow a'' = 2\).
Do đó, đường thẳng \(d''\) là \(y = 2x\).

a)
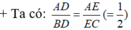
Nên theo định lí ta- let đảo ta có: DE // BC.
Nên theo định lí ta- let đảo ta có: EF // AB.
b) Tứ giác BDEF là hình bình hành vì có các cặp cạnh đối song song với nhau
c) Tứ giác BDEF là hình bình hành ⇒ DE = BF = 7
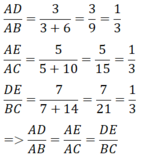
Ba cạnh của ΔADE tương ứng tỉ lệ với ba cạnh của ΔABC

a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
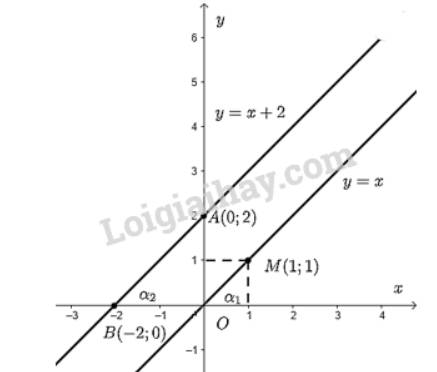
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).

Lời giải:
Vì đt $y=ax+b$ song song với $y=2x+2019$ nên $a=2$
$y=ax+b$ cắt trục tung tại điểm có tung độ $2020$, nghĩa là $(0,2020)\in (y=ax+b)$
$\Leftrightarrow 2020=a.0+b$
$\Rightarrow b=2020$
Vậy $a=2; b=2020$

Tọa độ giao điểm của hai đường thẳng y=x-7 và y=-4x+3 là:
\(\left\{{}\begin{matrix}x-7=-4x+3\\y=x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+4x=7+3\\y=x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=10\\y=x-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-7=-5\end{matrix}\right.\)
Thay x=2 và y=-5 vào y=ax+b, ta được:
a*2+b=-5
=>2a+b=-5(1)
thay x=-1 và y=-3 vào y=ax+b, ta được:
a*(-1)+b=-3
=>-a+b=-3(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=-5\\-a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=-2\\a-b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{2}{3}\\b=a-3=-\dfrac{2}{3}-3=-\dfrac{11}{3}\end{matrix}\right.\)
Vậy: (d): \(y=-\dfrac{2}{3}x-\dfrac{11}{3}\)

 và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.
và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.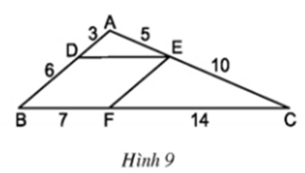
Khi hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là góc nhọn
Khi hệ số góc a âm thì góc tạo bởi đường thẳng này và trục Ox là góc tù.