Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải chi tiết:
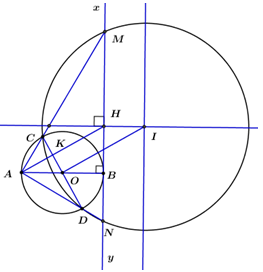
1) Chứng minh tứ giác MCDN nội tiếp.
Xét (O;R)(O;R) ta có: AB,CDAB,CD là hai đường kính của hình tròn
⇒ADBC⇒ADBC là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường).
⇒{AC=BDAD=BC⇒{AC=BDAD=BC (các cạnh đối).
Ta có: ∠ADB=900∠ADB=900 (góc nội tiếp chắn nữa đường tròn)
⇒∠BDN=900(1)⇒∠BDN=900(1)
Ta có: ∠CMN∠CMN là góc có đỉnh nằm ngoài đường tròn chắn các cung
BCBC và AB.AB.
⇒∠CMN=12(sdcungAB−sdcungCB)=12sdcungBD=12sdcungAC.(doAC=BD)⇒∠CMN=12(sdcungAB−sdcungCB)=12sdcungBD=12sdcungAC.(doAC=BD)
Lại có: ∠ADC∠ADC là góc nội tiếp chắn cung AC⇒∠ADC=12sdcungACAC⇒∠ADC=12sdcungAC
⇒∠ADC=∠CMN(=12sdcungAC).⇒∠ADC=∠CMN(=12sdcungAC).
⇒CDNM⇒CDNM là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện). (đpcm)
2) Chứng minh AC.AM=AN.AN.AC.AM=AN.AN.
Xét ΔACDΔACD và ΔANMΔANM ta có:
∠CADchung∠AMB=∠ADC(cmt)⇒ΔACD∼ΔANM(g−g)⇒ACAN=ADAM⇒AC.AM=AN.AD(dpcm).∠CADchung∠AMB=∠ADC(cmt)⇒ΔACD∼ΔANM(g−g)⇒ACAN=ADAM⇒AC.AM=AN.AD(dpcm).
3) Gọi I là tâm đường tròn nội tiếp tứ giác MCDN và H là trung điểm MN. Chứng minh tứ giác AOIH là hình bình hành. Khi đường kính CD quay quanh điểm O thì I di động trên đường nào?
Ta có I là tâm đường tròn nội tiếp tứ giác MCDN, H là trung điểm của MN
⇒IH⊥MN⇒IH⊥MN (mối quan hệ giữa đường kính và dây cung).
Mà AO⊥MNAO⊥MN (do AB là đường kính của đường tròn (O), MN là tiếp tuyến tại B của đường tròn)
⇒HI//AO(⊥MN)(1)⇒HI//AO(⊥MN)(1)
Mặt khác ta có ∠CAD=900∠CAD=900 (góc nội tiếp chắn nửa đường tròn)
⇒∠ACD+∠CDA=900⇒∠ACD+∠CDA=900 (tổng hai góc nhọn trong tam giác vuông)
Xét ΔMANΔMAN có ∠MAN=900∠MAN=900, H là trung điểm của MN
⇒AH=12MN=MH⇒AH=12MN=MH (đường trung tuyến ứng với cạnh huyền của tam giác vuông)
⇒ΔAHM⇒ΔAHM cân tại H (dhnb)
⇒∠MAH=∠HMA⇒∠MAH=∠HMA (hai góc kề đáy của tam giác cân).
Lại có : ∠ACD=∠CAB∠ACD=∠CAB (hai góc nội tiếp chắn hai cung AD, CB bằng nhau).
Mà : ∠AMH+∠CAB=900∠AMH+∠CAB=900 (tam giác ABM vuông tại B)
⇒∠MAH+∠ACD=900⇒ΔCAK⇒∠MAH+∠ACD=900⇒ΔCAK vuông tại K⇒CD⊥AH={K}.K⇒CD⊥AH={K}.
Lại có : OI⊥CDOI⊥CD (mối quan hệ giữa đường kính và dây cung)
⇒AH//OI(⊥CD).(2)⇒AH//OI(⊥CD).(2)
Từ (1) và (2) ta có : {AH//OIAO//HI⇒AOIH{AH//OIAO//HI⇒AOIH là hình bình hành (dhnb). (đpcm)
Ta có : HH là trung điểm của MN,M,NMN,M,N thuộc đườn thẳng xyxy cố định ⇒H⇒H là điểm di động trên đường xy.xy.
Vì AOIHAOIH là hình bình hành (cmt) ⇒AO=IH⇒AO=IH (hai cạnh đối)
Mà AO=RAO=R không đổi ⇒IH=R⇒IH=R không đổi.
⇒I⇒I là điểm di động trên đườgn thẳng song song với đường thẳng xy.xy.
4) Khi góc AHB bằng 600; Tính diện tích xung quanh của hình trụ tạo thành khi hình bình hành AHOI quay quanh cạnh AH theo R.
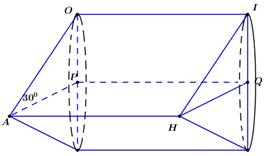
Ta có : ∠AHB=600⇒∠OAH=300∠AHB=600⇒∠OAH=300
Khi quay hình bình hành AHIO một vòng quanh cạnh AH thì cạnh AO và cạnh HI tạo nên hai hình nón bằng nhau có đường sinh AO=IH=R.AO=IH=R.
Cạnh OI tạo nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón cũng như bán kính của hình tròn (O)(O) là R.R.
Gọi P, Q là tâm các đường tròn đáy của hình trụ.
Xét ΔAOPΔAOP ta có : ∠OPA=900,∠OAP=300.∠OPA=900,∠OAP=300.
⇒sin300=OPOA=OPR⇒OP=Rsin300=R2.⇒sin300=OPOA=OPR⇒OP=Rsin300=R2.
Xét ΔABHΔABH ta có : AH=ABtan600=2R√3=2R√33.AH=ABtan600=2R3=2R33.
Diện tích xung quanh hình trụ cần tính là : Sxq=2πrh=2π.OP.AH=2π.R2.2R√33=2πR2√33.
a: Gọi O là trung điểm của AC
=>O là tâm đường tròn đường kính AC
Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó: ΔABC vuông tại B
=>BC\(\perp\)AB tại B
Xét (O) có
ΔADC nội tiếp
AC là đường kính
Do đó: ΔADC vuông tại D
=>AD\(\perp\)DC tại D
Xét ΔAEF có
FB,ED là các đường cao
FB cắt ED tại C
Do đó: C là trực tâm của ΔAEF
=>AC\(\perp\)EF
b: Xét ΔDFC vuông tại D và ΔDEA vuông tại D có
\(\widehat{DFC}=\widehat{DEA}\left(=90^0-\widehat{BAD}\right)\)
Do đó;ΔDFC~ΔDEA
=>\(\dfrac{DF}{DE}=\dfrac{DC}{DA}\)
=>\(DF\cdot DA=DC\cdot DE\)
c: Xét tứ giác BDFE có \(\widehat{EDF}=\widehat{EBF}=90^0\)
nên BDFE là tứ giác nội tiếp
Tứ giác ABCD nội tiếp đường tròn với đường kính AC có các tính chất sau:
a. EF vuông góc với AC: Điều này có thể được suy ra từ tính chất của tứ giác nội tiếp, trong đó tổng số đo hai góc đối diện bằng 180°.
b. DA . DF = DC . DE: Đây là một tính chất của tứ giác nội tiếp, nơi tích của độ dài hai cạnh không liên tiếp bằng nhau.
c. Tứ giác BDFE nội tiếp: Điều này có thể được chứng minh bằng cách sử dụng các tính chất của tứ giác nội tiếp, trong đó tổng số đo hai góc đối diện bằng 180°