Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B D O M S T L K E F
Nhận xét: Tứ giác ABCD nội tiếp đường tròn đường kính AC vì ^ABC=^CDA=900. Gọi tâm của đường tròn này là O. Khi đó thì O chính là trung điểm đoạn AC. Ta thấy M là 1 điểm chung của (S) và (T), đồng thời là trung điểm BD nên M nằm trên trung trực BD. Gọi giao điểm thứ hai của (S) và (T) là L. Ta đi chứng minh L cũng nằm trên trung trực BD. Thật vậy:
Từ M kẻ MK vuông góc với đường thẳng ST. Gọi E,F lần lượt là hình chiếu của S,T lên MA,MC.
Khi đó các tứ giác KSEM, KTMS nội tiếp => ^EKF = ^MKE + ^MKF = ^MSE + ^MTF = (^ASM + ^CTM)/2
Ta thấy AC là tiếp tuyến chung của (S) và (T) nên ^MAC = ^ASM/2; ^MCA = ^CTM/2
Từ đó: ^EKF = ^MCA + ^MAC = ^EOA + ^FOC (Chú ý tứ giác MEOF là hbh) = 1800 - ^EOF
Suy ra tứ giác KEOF nội tiếp => ^EKO = ^EFO = ^MAC = ^MSE (=^ASM/2) = ^EKM
Mà M và O nằm cùng phía so với EK nên tia KM,KO trùng nhau hay O,M,K thẳng hàng
Mặt khác: (S) và (T) cắt nhau tại M và L nên ML vuông góc ST. Do MK vuông góc ST nên M,K,L thẳng hàng
Vì vậy 4 điểm O,M,K,L thẳng hàng. Lại có OM là trung trực của BD => ML cũng là trung trực BD
Hay 2 giao điểm của (S) và (T) cùng nằm trên đường trung trực của BD (đpcm).

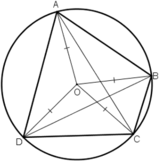
Tứ giác ABCD có 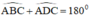
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
D A B C O
- Tứ giác ABCD có \(\widehat{ABC}+\widehat{ADC}=180^o\)mà hai góc ABC và ADC là 2 góc ở vị trí đối nhau
=> Tứ giác ABCD là tứ giác nội tiếp
- Gọi O là tâm của đường tròn ngoại tiếp tứ giác ABCD , khi đó OA = OB = OC = OD ( cùng bán kính của đường tròn ( O ))
+) Vì OA = OB nên O thuộc đường trung trực của đoạn thằng AB
+) Vì OA = OC nên O thuộc đường trung trực của đoạn thẳng AC
+) VÌ OD = OB nên O thuộc đường trung trực của đoạn thằng BD
Do đó các đường trung trực của AB , BD cùng đi qua tâm O của đường tròn ngoại tiếp tứ giác ABCD

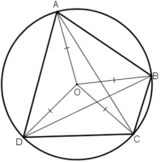
Tứ giác ABCD có 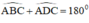
⇒ ABCD là tứ giác nội tiếp
Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
⇒ OA = OB = OC = OD = R
Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.
Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD
Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.
⇒ O thuộc đường trung trực của AC, BD, AB .
Vậy các đường trung trực của AC, BD, AB cùng đi qua O.
Kiến thức áp dụng
+ Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp một đường tròn.

Gọi P và Q lần lượt là trung điểm của AC' và CA'.
CC' giao MN tại I
Xét tam giác AC'C. P là trung điểm AC', M là trung điểm của AC
=> PM là đường trung bình tam giác AC'C => PM//CC'
hay C'I//PM
C' là trọng tâm tam giác ABD => C'N=AN/3.(T/c trọng tâm)
Mà P là trung điểm AC' => C' là trung điểm PN.
Xét tam giác PNM: C' là trung điểm PN, C'I//PM => I là trung điểm của MN
=> CC' đi qua trung điểm của MN (1)
Tương tự ta chứng minh được AA' đi qua trung điểm MN (2)
Tương tự xét trong tam giác DMB: BB' và DD' cùng đi qua trung điểm I của MN (3)
Từ (1),(2) và (3) => AA';BB';CC';DD',MN đồng quy (đpcm).
Bạn dựa theo dạng này
Vậy B nằm trên đường trung trực của đoạn thẳngAC (1)
Tương tự ta có AD=CD (gt)
Vậy D nằm trên đường trung trực của AC (2)
Từ (1) và (2) ta suy ra BD là đường trung trực của AC (đpcm)
b,ΔABD=ΔCBD(c.c.c)⇒ˆBAD=ˆBCDΔABD=ΔCBD(c.c.c)⇒BAD^=BCD^
Ta lại có :
ˆBAD+ˆBCD=3600−ˆB−ˆDBAD^+BCD^=3600−B^−D^
=3600−1000−700=1900=3600−1000−700=1900
do đó :ˆA=ˆC=1900:2=950

xét tg ABCD có \(\widehat{A}+\widehat{C}=180^0\)
\(\Rightarrow\)ABCD là tg nt (O) ( tg có tổng 2 góc đối = 1800 là tg nt )
xét (O) có \(\widehat{DAC}=\widehat{BAC}\)( AC là tia pg của \(\widehat{DAC}\))
\(\Rightarrow\)\(\widebat{DC}=\widebat{BC}\)(2 góc nt = nhau chắn 2 cung = nhau)
\(\Rightarrow\widehat{DBC}=\widehat{BDC}\)( 2 CUNG = NHAU CHẮN 2 GÓC NT = NHAU)
\(\Rightarrow\)\(\Delta BDC\)cân tại C
mà CK là đường trung tuyến của \(\Delta BDC\)(K là trung điểm của BD)
\(\Rightarrow\)CK đồng thời là đường cao , đường trung tuyến , tia pg của \(\Delta BDC\)
\(\Rightarrow\)\(CK\perp BD\) (1)
xét \(\Delta BDE\)là tam giác đều có CK là đường trung tuyến ( k là trung điểm của BD)
\(\Rightarrow\)EK đồng thời là đường cao , trung tuyến và tia phân giác của \(\Delta BDE\)
\(\Rightarrow EK\perp BD\) (2)
TỪ (1) VÀ (2) \(\Rightarrow\)E , C , K thẳng hàng
#mã mã#

Tứ giác ABCD có tổng hai góc đối diện bằng 180o nên nội tiếp đường tròn tâm O, ta có
OA = OB = OC = OD
Do đó các đường trung trực của AB, BD, AB cùng đi qua O
Tứ giác ABCD có tổng hai góc đối diện bằng 180o nên nội tiếp đường tròn tâm O, ta có
OA = OB = OC = OD
Do đó các đường trung trực của AB, BD, AB cùng đi qua O