Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác AEDF có
FD//AE(gt)
ED//AF(gt)
Do đó: AEDF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEDF có AD là tia phân giác của \(\widehat{FAE}\)(gt)
nên AEDF là hình thoi(Dấu hiệu nhận biết hình thoi)

1.
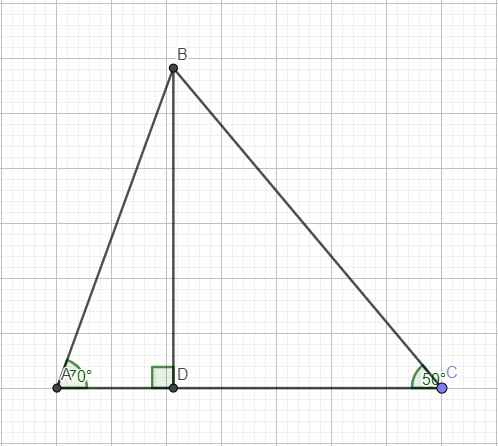
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
[ACD] = [ABCD] - [ABC] = 35,3554 cm2
kẻ BH _|_ AC ; DK_|_ AC cắt MN tại P
=> \(k=\frac{DP}{DK}=\frac{DP}{DK}-1+1=\frac{PK}{DK}+1=\frac{BH}{DK}+1=\frac{\left[ABC\right]}{\left[ACD\right]}+1=1,4399978504\)
[DMN]=k2 .[ADC] = .....tự tính nhé