Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

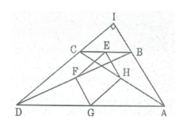
* Trong ∆ BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ∆ ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ∆ ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay ∠ (FEH) = 90 0
Vậy hình bình hành EFGH là hình chữ nhật.

+ Xét tg BCD có EF là đường trung bình => EF//=CD/2
+ Xét tg ACD có GH là đường trung bình => GH//=CD/2
=> EF//=GH => EFGH là hình bình hành (1)
+ Xét tg ABC có HE là đường trung bình => HE=AB/2 mà EF=CD/2 và AB=CD => EF=HE (2)
Từ 91) và (2) => EFGH là hình thoi => EG vuông góc với FH (2 đường chéo của hình thoi vuông góc với nhau)

Bạn xem lại đề bài xem, nếu đã là tứ giác ABCD thì không bao giờ AB vuông góc CD đâu.

Câu 2
A B C H D E M Xét ΔABC có
\(\left\{{}\begin{matrix}\text{M là trung điểm của BC}\\\text{D là trung điểm của AB}\end{matrix}\right.\)
⇒ MD là đường trung bình của ΔABC
⇒ MD = \(\dfrac{1}{2}\)AC (1)
Vì AH là đường cao của ΔABC
⇒ AH ⊥ BC
⇒ ΔAHC vuông tại H
Vì E là trung điểm của AC
⇒ HE là đường trung tuyến của ΔABC
Như vậy
\(\left\{{}\begin{matrix}\text{ΔAHC vuông tại H}\\\text{HE là đường trung tuyến của ΔABC}\end{matrix}\right.\)
⇒ HE = \(\dfrac{1}{2}\) AC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền) (2)
Từ (1), (2) ⇒ MD = HE (3)
Xét ΔABC có
\(\left\{{}\begin{matrix}\text{E là trung điểm của AC}\\\text{D là trung điểm của AB}\end{matrix}\right.\)
⇒ DE là đường trung bình của ΔABC
⇒ DE // BC
⇒ DE // HM
⇒ Tứ giác DEMH là hình thang (4)
Từ (3), (4) ⇒ Tứ giác DEMH là hình thang cân (đpcm)
Chúc bạn học tốt!!!@@@@@
Vì HG là đường trung bình của tam giác ACD nên HG // CD. Tương tự EF là đường trung bình của tam giác BCD nên EF // CD.