Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

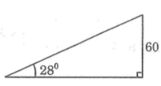
Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28 ° , chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
60.cotg 28 ° ≈ 112,844 (m)

ta có : góc ACB= góc CAx= 28 độ ( so le trong)
- BC= AB x Cot 28 = 112 (m)
Vậy...

Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28°, chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
60.cotg28° ≈ 112,844 (m)

Đặt tam giác ABC vuông tại A với B là đỉnh tháp
Áp dụng tslg trong tam giác ABC vuông tại A:
\(tanC=\dfrac{AB}{AC}\)
\(\Rightarrow tan30^0=\dfrac{26}{AC}\)
\(\Rightarrow AC=\dfrac{26}{tan30^0}=26\sqrt{3}\left(m\right)\)

A B c Đỉnh của tòa nhà Vị trí của ô tô
\(\Delta ABC,\)\(\hat{ABC}=90^o\) có: \(\tan \hat{ACB}=\)\(\frac{AB}{BC}\)(tỉ số lượng giác) \(\Leftrightarrow\tan28^o=\frac{60}{BC}\Leftrightarrow BC\approx112,84\left(m\right)\)
khoảng cách tư ô tô đến tòa nhà là = \(\tan28\) độ \(\times\) 60=31,9 m

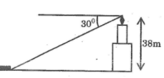
Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30 ° , chiều cao của cột đèn biển là cạnh đối diện với góc 30 °
Vậy khoảng cách từ đảo đến chân đèn là:
38.cotg 30 ° ≈ 65,818 (cm)
Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28∘∘, chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
\(60.cot28^o\approx112,844\left(m\right)\)
Vậy...