Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

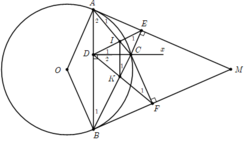
o D C A B E F x M I K
a) Ta có CD vuông AB => \(\widehat{CDA}=90^o\)
CE vuông AM => \(\widehat{CEA}=90^o\)
Xét tứ giác ADCE có :\(\widehat{CDA}+\widehat{CEA}=90^o+90^o=180^o\)
=> Tứ giác ADCE nội tiếp
b) Tương tự ta chứng minh được tứ giác CDBF nội tiếp
Tứ giác ADCE nội tiếp => \(\widehat{CDE}=\widehat{CAE}\)( cùng chắn cung CE)
Tứ giác CDBF nội tiếp => \(\widehat{CFD}=\widehat{CBD}\)( cùng chắn cung DC)
Mà \(\widehat{CBD}=\widehat{CAE}\)( cùng chắn cung AC của đường tròn (O))
=> \(\widehat{CDE}=\widehat{CFD}\)
Tương tự như trên ta chứng minh được : \(\widehat{DEC}=\widehat{DAC}=\widehat{CBF}=\widehat{FDC}\)
Xét tam giác CDE và tam giác CFD có:
\(\widehat{CDE}=\widehat{CFD}\)
\(\widehat{DEC}=\widehat{FDC}\)
=> \(\Delta CDE=\Delta CFD\)
3) Gọi Cx là tia đối của ta CD
Nối OM. Dễ dàng chứng minh được: OM vuông AB, \(\widehat{AOM}=\widehat{BOM}\)(1)
Ta có: Cx//OM ( cùng vuông góc với AB), CE//OA ( cùng vuông với AM)
=> \(\widehat{AOM}=\widehat{ECx}\)(2)
Cx// OM, CF//OB ( cùng vuông với BM)
=> \(\widehat{BOM}=\widehat{FCx}\)(3)
Từ (1), (2), (3),
=> \(\widehat{ECx}=\widehat{FCx}\)
=> Cx là phân giác góc ECF
4. Ở câu 2 Ta đã chứng minh : \(\widehat{CDE}=\widehat{CBD}\Rightarrow90^o=\widehat{DCB}+\widehat{CBD}=\widehat{CDE}+\widehat{DCB}=\widehat{CDI}+\widehat{DCK}\)
Tương tự như trên chứng minh được: \(\widehat{CDK}+\widehat{ICD}=90^o\)
Xét tứ giác IDKC có: \(\widehat{IDK}+\widehat{ICK}=\widehat{IDC}+\widehat{CDK}+\widehat{ICD}+\widehat{DCK}=\left(\widehat{IDC}+\widehat{DCK}\right)+\left(\widehat{CDK}+\widehat{ICD}\right)\)
\(=90^o+90^o=180^o\)
=> Tứ giác IDKC nội tiếp
=> \(\widehat{IKC}=\widehat{IDC}=\widehat{DBC}\)
=> IK//AB ( 2 góc so le trong)

1) Hình vẽ câu 1) đúng
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B


( mấy cái cơ bản thì tự viết nhé )
a) góc MAO và góc MBO= 90 độ
xét tứ giác MAOB có góc MAO+MBO=180 độ
=> MAOB nội tiếp
b) Xét (O) có EB là tiếp tuyến của (O)
\(\Rightarrow\widehat{EBD}=\widehat{EAB}\left(=\frac{1}{2}sđ\widebat{DB}\right)\)
Xét tam giác EDB và tam giác EBA có:
\(\hept{\begin{cases}\widehat{AEB}chung\\\widehat{EBD}=\widehat{EAB}\left(cmt\right)\end{cases}\Rightarrow\Delta EDB~\Delta EBA\left(g-g\right)}\)
\(\Rightarrow\frac{BE}{DE}=\frac{AE}{BE}\)
\(\Rightarrow BE^2=AE.DE\left(1\right)\)
Vì \(AC//MB\Rightarrow\widehat{ACM}=\widehat{DME}\left(SLT\right)\)
Ta có: \(\hept{\begin{cases}\widehat{ACM}=\widehat{ABD}\left(=\frac{1}{2}sđo\widebat{AD}\right)\\\widehat{ABD}=\widehat{MAD}\left(=\frac{1}{2}sđo\widebat{AD}\right)\end{cases}\Rightarrow\widehat{ACM}=\widehat{MAD}}\)
\(\Rightarrow\widehat{DME}=\widehat{MAD}\)
Xét tam giác EMD và tam giác EAM có:
\(\hept{\begin{cases}\widehat{DME}=\widehat{MAD}\\\widehat{AME}chung\end{cases}}\Rightarrow\Delta EMD~\Delta EAM\left(g-g\right)\)
\(\Rightarrow\frac{ME}{DE}=\frac{AE}{ME}\)
\(\Rightarrow ME^2=DE.AE\left(2\right)\)
Từ (1) và (2) \(\Rightarrow BE=ME\left(đpcm\right)\)
c) mai nốt :V
c) El à trung điểm MB;H là trung điểm AB
-> EH là đường trung bình tam giác MAB
=> EH// MA
=> góc EHB= góc MAB ( đồng vị )
Mà góc MAB = góc AKB ( = 1/2 số đo cung AB )
=> góc EHB= góc AKB
mà góc EHB+ góc IHB = 180 độ
=> góc AKB + góc IHB = 180 độ
=> BHIK nội tiếp
=> góc BHK= BIK mà góc BHK= 90 độ
=> góc BIK= 90 độ
=> AK vuông góc với BI
sao khó vậy