Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

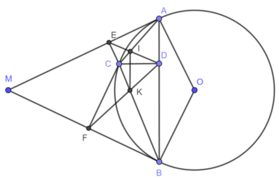
1) Hình vẽ câu 1) đúng
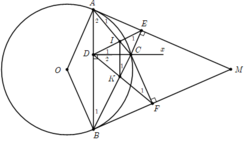
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

o D C A B E F x M I K
a) Ta có CD vuông AB => \(\widehat{CDA}=90^o\)
CE vuông AM => \(\widehat{CEA}=90^o\)
Xét tứ giác ADCE có :\(\widehat{CDA}+\widehat{CEA}=90^o+90^o=180^o\)
=> Tứ giác ADCE nội tiếp
b) Tương tự ta chứng minh được tứ giác CDBF nội tiếp
Tứ giác ADCE nội tiếp => \(\widehat{CDE}=\widehat{CAE}\)( cùng chắn cung CE)
Tứ giác CDBF nội tiếp => \(\widehat{CFD}=\widehat{CBD}\)( cùng chắn cung DC)
Mà \(\widehat{CBD}=\widehat{CAE}\)( cùng chắn cung AC của đường tròn (O))
=> \(\widehat{CDE}=\widehat{CFD}\)
Tương tự như trên ta chứng minh được : \(\widehat{DEC}=\widehat{DAC}=\widehat{CBF}=\widehat{FDC}\)
Xét tam giác CDE và tam giác CFD có:
\(\widehat{CDE}=\widehat{CFD}\)
\(\widehat{DEC}=\widehat{FDC}\)
=> \(\Delta CDE=\Delta CFD\)
3) Gọi Cx là tia đối của ta CD
Nối OM. Dễ dàng chứng minh được: OM vuông AB, \(\widehat{AOM}=\widehat{BOM}\)(1)
Ta có: Cx//OM ( cùng vuông góc với AB), CE//OA ( cùng vuông với AM)
=> \(\widehat{AOM}=\widehat{ECx}\)(2)
Cx// OM, CF//OB ( cùng vuông với BM)
=> \(\widehat{BOM}=\widehat{FCx}\)(3)
Từ (1), (2), (3),
=> \(\widehat{ECx}=\widehat{FCx}\)
=> Cx là phân giác góc ECF
4. Ở câu 2 Ta đã chứng minh : \(\widehat{CDE}=\widehat{CBD}\Rightarrow90^o=\widehat{DCB}+\widehat{CBD}=\widehat{CDE}+\widehat{DCB}=\widehat{CDI}+\widehat{DCK}\)
Tương tự như trên chứng minh được: \(\widehat{CDK}+\widehat{ICD}=90^o\)
Xét tứ giác IDKC có: \(\widehat{IDK}+\widehat{ICK}=\widehat{IDC}+\widehat{CDK}+\widehat{ICD}+\widehat{DCK}=\left(\widehat{IDC}+\widehat{DCK}\right)+\left(\widehat{CDK}+\widehat{ICD}\right)\)
\(=90^o+90^o=180^o\)
=> Tứ giác IDKC nội tiếp
=> \(\widehat{IKC}=\widehat{IDC}=\widehat{DBC}\)
=> IK//AB ( 2 góc so le trong)

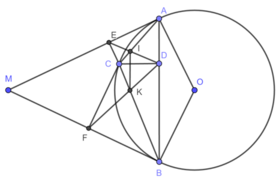

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC) (2)

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung CB) (5)


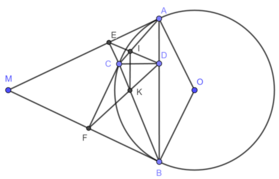

( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)

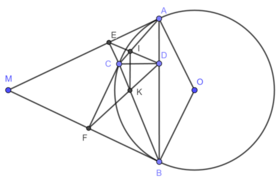


gọi G là giao của tia đối tia CD với AM (ta giả sử cung AC < cung BC)
ý c: từ b suy ra tam giác CDE đồng dạng CFD
=> \(\widehat{ECD}=\widehat{FCD}\)
ta có: \(\widehat{ECD}+\widehat{GCE}=180^o\)
\(\widehat{FCD}+\widehat{GCF}=180^o\)
\(\widehat{GCE}=\widehat{GCF}\)suy ra đccm
ý d: CM IK//AB
Ta có: \(\widehat{FDB}=\widehat{FCB}\)(BDCF nôi tiếp đường tròn)
\(\hept{\begin{cases}\widehat{FCB}+\widehat{FBC}=90^o\\\widehat{DCA}+\widehat{CAD}=90^o\end{cases}}\)
mà \(\widehat{CAD}=\widehat{FBC}\)(cùng chắn cung BC)
\(\Rightarrow\widehat{FCB}=\widehat{DCA}\Rightarrow\widehat{FDB}=\widehat{DCA}\)(1)
Tương tự:
\(\hept{\begin{cases}\widehat{ECA}+\widehat{EAC}=90^o\\\widehat{DCB}+\widehat{DBC}=90^o\end{cases}}\)
mà \(\widehat{EAC}=\widehat{DBC}\)(cùng chắn cung AC)
\(\Rightarrow\widehat{ECA}=\widehat{DCB}\). mà \(\widehat{ECA}=\widehat{EDA}\)(tứ giác ECDA nội tiếp nên 2 góc kia cùng chắn cung AE)
\(\Rightarrow\widehat{DCB}=\widehat{EDA}\)(2)
(1)+(2) => \(\widehat{ACD}+\widehat{BCD}=\widehat{FDB}+\widehat{EDA}\)
\(\Rightarrow\widehat{ICK}=\widehat{FDB}+\widehat{EDA}\)\(\Rightarrow\widehat{ICK}+\widehat{IDK}=\widehat{FDB}+\widehat{EDA}+\widehat{IDK}=180^o\)
suy ra tứ giác IDKC nội tiếp \(\Rightarrow\widehat{CKI}=\widehat{CDI}=\widehat{CAE}=\widehat{CBA}\)
mà góc CKI và góc CBA ở vị trí đồng vị suy ra IK//AB. ta đc đccm.