Question

[Minh Bình]

Từ A ngoài (O), bán kính R, vẽ tiếp tuyến AE và dây EF vuông góc với OA tại M

a) cho R =10cm,OM =6cm. Tính EF

b) c/m AF là tiếp tuyến của (O)

c) kẻ đường kính EC, tiếp tuyến với (O) tại C cắt EF tại D. Tính EM.ED theo R

d) kẻ tiếp tuyến DB. c/m A,B,C thẳng hàng

Answer 1

[Nguyễn Lê Phước Thịnh]

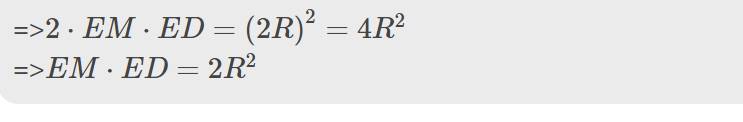
a: Xét ΔOEA vuông tại E có EM là đường cao

nên \(OM\cdot OA=OE^2\)

=>\(OA=\dfrac{10^2}{6}=\dfrac{50}{3}\left(cm\right)\)

ΔOEA vuông tại E

=>\(OE^2+EA^2=OA^2\)

=>\(EA^2+10^2=\left(\dfrac{50}{3}\right)^2\)

=>\(EA^2=\left(\dfrac{40}{3}\right)^2\)

=>EA=40/3(cm)

Xét ΔEAO vuông tại E có EM là đường cao

nên \(EM\cdot OA=EA\cdot EO\)

=>\(EM\cdot\dfrac{50}{3}=10\cdot\dfrac{40}{3}\)

=>\(EM\cdot50=10\cdot40\)

=>EM=400/50=8(cm)

Ta có: ΔOEF cân tại O

mà OM là đường cao

nên M là trung điểm của EF và OM là phân giác của góc EOF

=>\(EF=2\cdot EM=16\left(cm\right)\)

b: Xét ΔOEA và ΔOFA có

OE=OF
\(\widehat{EOA}=\widehat{FOA}\)

OA chung

Do đó: ΔOEA=ΔOFA

=>\(\widehat{OEA}=\widehat{OFA}=90^0\)

=>AFlà tiếp tuyến của (O)

c: Xét (O) có

ΔEFC nội tiếp

EC là đường kính

Do đó: ΔEFC vuông tại F

=>EF\(\perp\)FC tại F

=>CF\(\perp\)ED tại F

Xét ΔECD vuông tại C có EF là đường cao

nên \(EF\cdot ED=EC^2\)

=>\(2\cdot EM\cdot ED=\left(2R\right)^2=4R^2\)

=>\(EM\cdot ED=2R^2\)