Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 △BEC có AD//BE
△BEC có AD//BE
=> AD/BE = DC/BC (hệ quả thales) (1)
△BFC có AD//FC
=> AD/FC = BD/BC (hệ quả thales) (2)
Từ (1) và (2) cộng vế theo vế, ta đc:
AD/BE + AD/FC = DC/BC + BD/BC
Mà DC = BD (D là trung điểm BC)
=> AD/BE + AD/FC = 1
=> AD.(1/BE + 1/FC) = 1
=> 1/BE + 1/FC = 1/AD
Note: Đề của bạn thiếu điều kiện D là trung điểm của BC òi nha.

A B C D E F I K
a) Áp dụng hệ quả định lý \(Ta-lét\) vào \(\Delta BEC\) có \(AD//BE\left(gt\right)\) \(\Rightarrow\dfrac{AD}{BE}=\dfrac{CD}{BC}\left(2\right)\)
Áp dụng hệ quả định lý \(Ta-lét\) vào \(\Delta BFC\) có \(AD//CF\left(gt\right)\) \(\Rightarrow\dfrac{AD}{CF}=\dfrac{BD}{BC}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\dfrac{AD}{BE}+\dfrac{AD}{CF}=\dfrac{CD}{BC}+\dfrac{BD}{BC}\)
\(\Rightarrow AD\left(\dfrac{1}{BE}+\dfrac{1}{CF}\right)=\dfrac{CD+BD}{BC}=\dfrac{BC}{BC}=1\\ \Rightarrow\dfrac{1}{BE}+\dfrac{1}{CF}=\dfrac{1}{AD}\left(đpcm\right)\)
b) Áp dụng hệ quả định lý \(Ta-lét\) vào \(\Delta BAE\) có \(BE//CF\left(gt\right)\) \(\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{\: AB}\)
Xét \(\Delta EAF\) và \(\Delta CAB\) có: \(\left\{{}\begin{matrix}\dfrac{AE}{AC}=\dfrac{AF}{\: AB}\left(\text{Chứng minh trên}\right)\\\widehat{EAF}=\widehat{CAB}\left(\text{2 góc đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta EAF\sim\Delta CAB\left(c.g.c\right)\\ \Rightarrow\widehat{AEF}=\widehat{ACB}\left(\text{2 góc tương ứng}\right)\\ \Rightarrow EF//BC\left(\text{2 góc so le trong}\right)\)
Mà \(BE//CF\left(gt\right)\)
\(\Rightarrow\text{Tứ giác }BECF\text{ là hình bình hành}\left(\text{Dấu hiệu nhận biết}\right)\\ \Rightarrow A\text{ là trung điểm }EC\left(\text{Tính chất đường chéo hình bình hành}\right)\\ \Rightarrow AC=\dfrac{1}{2}AE\\ \Rightarrow S_{ABC}=\dfrac{1}{2}S_{BEC}\left(\text{Chung đường cao hạ từ B xuống EC}\right)\left(5\right)\)
Từ \(E\) kẻ \(EI\perp BC\Rightarrow EI\) là đường cao ứng với \(BC\) của \(\Delta EBC\)
Từ \(D\) kẻ \(DK\perp EF\Rightarrow DK\) là đường cao ứng với \(EF\) của \(\Delta EDF\)
Ta có : \(DI//EK\left(I\in BC;K\in EF;BC//EF\right)\left(3\right)\)
\(\Rightarrow EI\perp EK\left(EI\perp DI\right)\\ \Rightarrow EI//DK\left(\text{Cùng }\perp EK\right)\left(4\right)\)
Từ \(\left(3\right)\) và \(\left(4\right)\Rightarrow\text{Tứ giác }DIEK\text{ là hình bình hành}\left(\text{Dấu hiệu nhận biết}\right)\)\(\Rightarrow DI=EK\left(\text{2 cạnh đối hình bình hành}\right)\)
Mà \(EF=BC\left(\text{2 cạnh đối hình bình hành}\right)\)
\(\Rightarrow S_{DEF}=S_{EBC}\left(6\right)\)
Từ \(\left(5\right)\) và \(\left(6\right)\Rightarrow S_{ABC}=\dfrac{1}{2}S_{DEF}\)
\(\Rightarrow S_{DEF}=2S_{ABC}\left(đpcm\right)\)

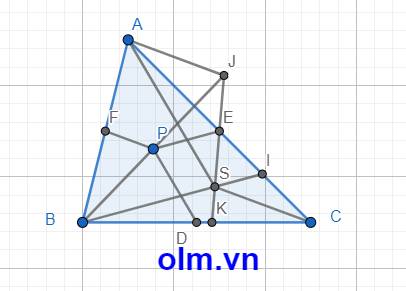
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:
PE // BS; PE = \(\dfrac{1}{2}\) BS
⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)
⇒ PJ = PB; EJ = ES (1)
Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB theo (1)
⇒ PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)
⇒ PF// AJ (2)
Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo
AE = EC (gt)
EJ = ES ( theo (1)
⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ CS // CJ (3)
Kết hợp (2) và(3) ta có:
CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)
Kết luận: nếu BS = 2EP thì CS // PF điều phải chứng minh

