Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Việc lựa chọn tiến hành theo hai bước (công đoạn) sau:
Bước 1: Chọn 4 học sinh nam từ 25 học sinh nam của lớp.
Số cách chọn này bằng số các tổ hợp chập 4 của 25, bằng ![]() cách.
cách.
Bước 2: Chọn 2 học sinh nữ từ 15 học sinh nữ của lớp.
Số cách chọn này bằng số các tổ hợp chập 2 của 15, bằng ![]() cách.
cách.
Theo quy tắc nhân, số cách lựa chọn của giáo viên là: ![]() =1328250cách.
=1328250cách.
Chọn A

Chọn B.
Số phần tử của không gian mẫu:
![]()
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: ![]()
![]() .
.

Đáp án B
Phương pháp: Xác suất : P ( A ) = n ( A ) n ( Ω )
Cách giải:
Số phần tử của không gian mẫu : n ( Ω ) = C 15 + 10 4 = C 25 4
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó :
![]()
Xác suất cần tìm:
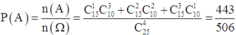

Đáp án: D.
![]()
Số cách chọn 3 học sinh có cả nam và nữ là
![]() .
.
Do đó xác suất để 3 học sinh được hcọn có cả nam và nữ là 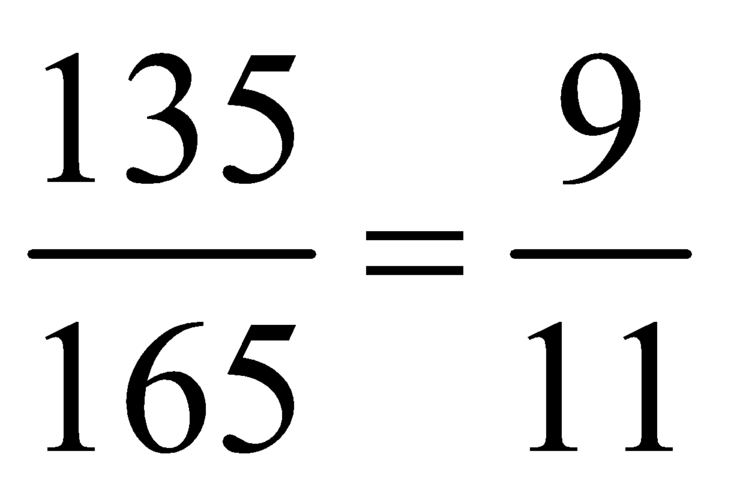 .
.

Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A ¯ là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là ![]()
Ta có ![]()
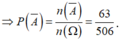
Vậy xác suất của biến cố A là
![]()

Đáp án : A
Để lựa chọn được hai ban thỏa mãn yêu cầu, ta chia làm hai công đoạn.
Công đoạn 1: Chọn một học sinh giỏi nữ, có 9 cách thực hiện.
Công đoạn 2. Chọn một học sinh giỏi nam, có 7 cách thực hiện.
Vậy theo quy tắc nhân, sẽ có 9.7=63 cách lựa chọn.

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
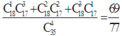

Lời giải:
Gọi A là biến cố sinh viên đó là nữ và B là biến cố sinh viên đó học khoa kinh tế -qtkd.
Theo bài ra:
$P(A)=0,6$
$P(B)=0,4$
$P(AB)=0,6.0,35=0,21$
a.
$P(A|B)=\frac{P(AB)}{P(B)}=\frac{0,21}{0,4}=0,525$
b.
$P(B|A)=\frac{P(AB)}{P(A)}=\frac{0,21}{0,6}=0,35$