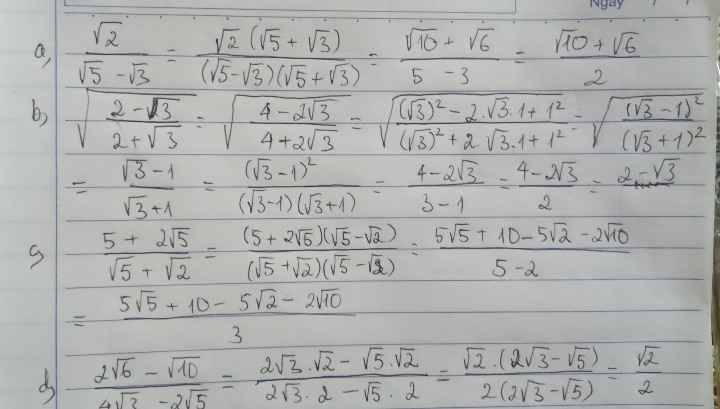Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{2}.\sqrt{2}}=\dfrac{\sqrt{10}-\sqrt{6}}{2}\)
b. \(\dfrac{26}{5-2\sqrt{3}}=\dfrac{26\left(5+2\sqrt{3}\right)}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}=\dfrac{26\left(5+2\sqrt{3}\right)}{13}=2\left(5+2\sqrt{3}\right)=10+4\sqrt{3}\)
c. \(\dfrac{2\sqrt{10}-5}{4-\sqrt{10}}=\dfrac{\left(2\sqrt{10}-5\right)\left(4+\sqrt{10}\right)}{\left(4-\sqrt{10}\right)\left(4+\sqrt{10}\right)}=\dfrac{3\sqrt{10}}{6}=\dfrac{\sqrt{10}}{2}\)
d. \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}=\dfrac{\left(9-2\sqrt{3}\right)\left(3\sqrt{6}+2\sqrt{2}\right)}{\left(3\sqrt{6}-2\sqrt{2}\right)\left(3\sqrt{6}+2\sqrt{2}\right)}=\dfrac{23\sqrt{6}}{46}=\dfrac{\sqrt{6}}{2}\)

Bài 50:
\(\dfrac{5}{\sqrt{10}}=\dfrac{5\sqrt{10}}{10}=\dfrac{\sqrt{10}}{2}\)
\(\dfrac{5}{2\sqrt{5}}=\dfrac{\sqrt{5}}{2}\)
\(\dfrac{1}{3\sqrt{20}}=\dfrac{1}{6\sqrt{5}}=\dfrac{\sqrt{5}}{30}\)
\(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}=\dfrac{\sqrt{2}\left(2+\sqrt{2}\right)}{5\sqrt{2}}=\dfrac{2+\sqrt{2}}{5}\)

mấy bài dạng này bn nên sử dụng cách nhân liên hợp hoặc phân tích đa thức thành nhân tử nha . mk lm 1 bài còn lại thì bn tự lm cho quen nha :)
a) ta có : \(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}-\sqrt{7}}=\dfrac{\left(\sqrt{6}+\sqrt{14}\right)\left(2\sqrt{3}+\sqrt{7}\right)}{\left(2\sqrt{3}-\sqrt{7}\right)\left(2\sqrt{3}+\sqrt{7}\right)}\)
\(=\dfrac{6\sqrt{2}+\sqrt{42}+2\sqrt{42}+7\sqrt{2}}{\left(2\sqrt{3}\right)^2-\left(\sqrt{7}\right)^2}=\dfrac{13\sqrt{2}+3\sqrt{42}}{5}\)
gợi ý : b) phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức số \(6\)
c) nhân liên hợp 2 lần nha .
a) \(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}-\sqrt{7}}\)
=\(\dfrac{\left(\sqrt{6}+\sqrt{14}\right)\left(2\sqrt{3}+\sqrt{7}\right)}{\left(2\sqrt{3}-\sqrt{7}\right).\left(2\sqrt{3}+\sqrt{7}\right)}\)
=\(\dfrac{\left(\sqrt{6}+\sqrt{14}\right).\left(2\sqrt{3}+\sqrt{7}\right)}{12-7}\)
=\(\dfrac{2\sqrt{18}+\sqrt{42}+2\sqrt{42}+\sqrt{98}}{5}\)
=\(\dfrac{6\sqrt{2}+\sqrt{42}+2\sqrt{42}+7\sqrt{2}}{5}\)
=\(\dfrac{3\sqrt{42}+13\sqrt{2}}{5}\)
b) \(\dfrac{5\sqrt{5}+3\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
=\(\dfrac{\left(5\sqrt{5}+3\sqrt{3}\right).\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right).\left(\sqrt{5}-\sqrt{3}\right)}\)
=\(\dfrac{25-5\sqrt{15}+3\sqrt{15}-9}{2}\)
=\(\dfrac{16-2\sqrt{15}}{2}=8-\sqrt{15}\)
Câu c mk chưa làm được![]()

bài 2:
a: \(\dfrac{25}{5-2\sqrt{3}}=\dfrac{125+10\sqrt{3}}{13}\)
b: \(\dfrac{8}{\sqrt{5}+2}=8\sqrt{5}-32\)
c: \(\dfrac{6}{2\sqrt{3}-\sqrt{7}}=\dfrac{12\sqrt{3}+6\sqrt{7}}{5}\)
d: \(=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}=\dfrac{\sqrt{6}}{2}\)

c) \(\dfrac{3\sqrt{3}}{\sqrt{2}+\sqrt{3}+\sqrt{5}}=\dfrac{3\sqrt{3}}{\left(\left(\sqrt{2}+\sqrt{3}\right)+\sqrt{5}\right)}=\dfrac{3\sqrt{3}\left(\left(\sqrt{2}+\sqrt{3}\right)-\sqrt{5}\right)}{\left(\left(\sqrt{2}+\sqrt{3}\right)+\sqrt{5}\right)\left(\left(\sqrt{2}+\sqrt{3}\right)-\sqrt{5}\right)}\) = \(\dfrac{3\sqrt{6}+9-3\sqrt{15}}{\left(\sqrt{2}+\sqrt{3}\right)^2-5}\) = \(\dfrac{3\sqrt{6}+9-3\sqrt{15}}{2+2\sqrt{6}+3-5}=\dfrac{3\sqrt{6}+9-3\sqrt{15}}{2\sqrt{6}}\)
= \(\dfrac{\left(3\sqrt{6}+9-3\sqrt{15}\right)\sqrt{6}}{2\sqrt{6}.\sqrt{6}}\) = \(\dfrac{18+9\sqrt{6}-9\sqrt{10}}{12}\)
= \(\dfrac{3\left(6+3\sqrt{6}-3\sqrt{10}\right)}{3.4}=\dfrac{6+3\sqrt{6}-3\sqrt{10}}{4}\)
d) \(\dfrac{4}{1+\sqrt{2}+\sqrt{3}}=\dfrac{4}{\left(\left(1+\sqrt{2}\right)+\sqrt{3}\right)}=\dfrac{4\left(\left(1+\sqrt{2}\right)-\sqrt{3}\right)}{\left(\left(1+\sqrt{2}\right)+\sqrt{3}\right)\left(\left(1+\sqrt{2}\right)-\sqrt{3}\right)}\)
= \(\dfrac{4+4\sqrt{2}-4\sqrt{3}}{\left(1+\sqrt{2}\right)^2-3}=\dfrac{4+4\sqrt{2}-4\sqrt{3}}{1+2\sqrt{2}+1-3}\) = \(\dfrac{4+4\sqrt{2}-4\sqrt{3}}{2\sqrt{2}}\)
\(\dfrac{\left(4+4\sqrt{2}-4\sqrt{3}\right)\sqrt{2}}{2\sqrt{2}\sqrt{2}}=\dfrac{4\sqrt{2}+8-4\sqrt{6}}{4}\) = \(\dfrac{4\left(\sqrt{2}+4-\sqrt{6}\right)}{4}=\sqrt{2}+4-\sqrt{6}\)
câu a thôi nha
câu b:\(\dfrac{1}{\sqrt{3}+\sqrt{2}+\sqrt{5}}=\dfrac{\sqrt{3}+\sqrt{2}-\sqrt{5}}{\left(\sqrt{3}+\sqrt{2}+\sqrt{5}\right)\left(\sqrt{3}+\sqrt{2}-\sqrt{5}\right)}\)
\(=\dfrac{\sqrt{3}+\sqrt{2}-\sqrt{5}}{2\sqrt{6}}=\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}-\sqrt{5}\right)}{12}=\dfrac{3\sqrt{2}+2\sqrt{3}-\sqrt{30}}{12}\)
câu c,d tương tự câu b thôi
bản chất lười =))

câu e mình viết sai đề, mk sửa lại nhé , với mình bổ sung câu f
e) \(\dfrac{2}{\sqrt[3]{4}+\sqrt[3]{5}}\)
f) \(\dfrac{1}{2-\dfrac{\sqrt[3]{3}}{2}}\)

bạn nên tự nghiên cứu rồi giải đi chứ bạn đưa 1 loạt thế thì ai rảnh mà giải, với lại cứ bài gì không biết chưa chịu suy nghĩ đã hỏi rồi thì tiến bộ sao được, đúng không

\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}=\dfrac{\left(\sqrt{5}-1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}=\dfrac{5-2\sqrt{5}+1}{5-1}=\dfrac{2\left(3-\sqrt{5}\right)}{4}=\dfrac{3-\sqrt{5}}{2}\)
b: \(\dfrac{37}{7+2\sqrt{3}}=7-2\sqrt{3}\)
c:\(=\dfrac{\sqrt{5}\left(2\sqrt{2}-\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{2}-\sqrt{5}\right)}=\sqrt{\dfrac{5}{2}}=\dfrac{\sqrt{10}}{2}\)
d: \(=\dfrac{\left(1+\sqrt{a}\right)\cdot\left(2+\sqrt{a}\right)}{4-a}\)

Bài 1 bạn nhóm , trục như thường nhé :D
Bài 2. \(a.A=\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}=\sqrt{3+2\sqrt{3}.\sqrt{2}+2}-\sqrt{3-2\sqrt{3}.\sqrt{2}+2}=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\)
\(b.B=\sqrt{17-12\sqrt{2}}-\sqrt{9+4\sqrt{2}}=\sqrt{9-2.2\sqrt{2}.3+8}-\sqrt{8+2.2\sqrt{2}+1}=3-2\sqrt{2}-2\sqrt{2}-1=2-4\sqrt{2}\)
\(c.C=\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{8+2.2.\sqrt{2}+1}}}=\sqrt{13+30\sqrt{2+2\sqrt{2}+1}}=\sqrt{43+30\sqrt{2}}=\sqrt{25+2.3\sqrt{2}.5+18}=5+3\sqrt{2}\)
\(d.D=\sqrt{12-3\sqrt{7}}-\sqrt{12+3\sqrt{7}}\)
\(D^2=24-2\sqrt{\left(12-3\sqrt{7}\right)\left(12+3\sqrt{7}\right)}=24-2\sqrt{81}=24-18=6\)
\(D=-\sqrt{6}\left(do:D< 0\right)\)