Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu này dễ mak
Ta có tam giác vuông có 3 cạnh b,c,a với h là đường cao ứng với cạnh huyền a, ta có
+) b^2 + c^2 = a^2 (Định lí Pi-ta-go)
+) ah = bc(Hệ thức lượng)
Ta có:
+) (b + c)^2 + h^2 = b^2 + 2bc + c^2 + h^2 = a^2 + 2ah + h^2
+) (a + h)^2 = a^2 + 2ah + h^2
Từ đây suy ra: (b + c)^2 + h^2 = (a + h)^2
=> Tam giác có 3 cạnh là b + c; a+ h và h là tam giác vuông (Định lí Py-ta-go đảo)

- Giả sử tam giác ABC vuông tại A . Theo bài ra , ta có :
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\left(1\right)\)
- Áp dụng đlí Py - ta - go cho tam giác vuông ABC ( \(\widehat{A}=90^o\))
Ta có : \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow125^2=\left(\frac{3}{4}AC\right)^2+AC^2\)
\(\Leftrightarrow15625=\frac{9}{16}AC^2+AC^2\)
\(\Leftrightarrow15625=\left(\frac{9}{16}+1\right)AC^2\)
\(\Leftrightarrow\frac{25}{16}AC^2=15625\)
\(\Leftrightarrow AC^2=\frac{15625.16}{25}\)
\(\Leftrightarrow AC=\sqrt{\frac{15625.16}{25}}=\frac{125.4}{5}=100\left(cm\right)\)
Thay AC = 100cm vào (1) , ta được :
\(AB=\frac{3}{4}.100=75\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) đường cao AH , ta có :
\(AB^2=BH.BC\)
\(\Leftrightarrow BH=\frac{AB^2}{BC}=\frac{75^2}{125}=45\left(cm\right)\)
Ta lại có : BC = BH + HC
125 = 45 + HC
HC = 125 - 45 = 80 ( cm )
Vậy : AB = 75 cm
AC = 100 cm
HC = 80 cm
BH = 45 cm

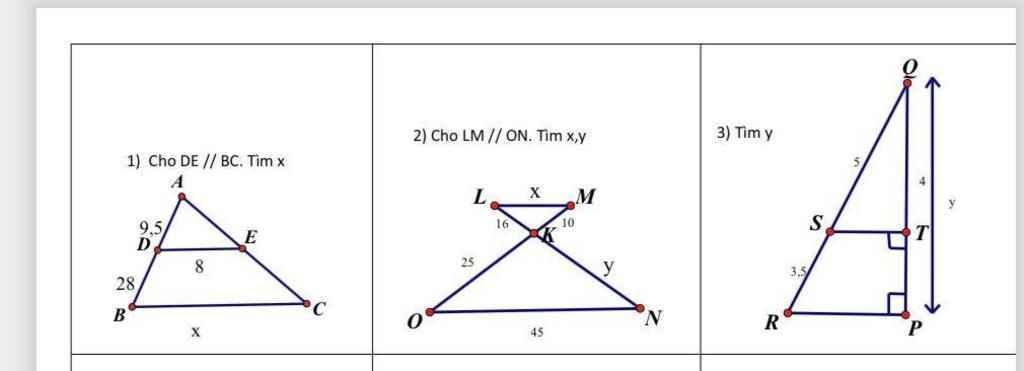
`1).`
Ta có: `AB=AD+DB=9,5+28=37,5`
`\triangle ABC` có: `DE////BC`, theo hệ quả của định lí Ta-lét:
`(AD)/(AB)=(DE)/(BC)`
`=>(9,5)/(37,5)=8/x`
`=>x=(37,5.8)/(9,5)`
`=>x=600/19`
`2).`
`\triangle OKN` có: `LM////ON` theo hệ quả của định lí Ta-lét:
`(KO)/(KM)=(KN)/(KL)=(ON)/(LM)`
`=>25/10=y/16=45/x`
`=>y/16=45/x=5/2`
Với `y/16=5/2=>y=(16.5)/2=40`
Với `45/x=5/2=>x=(45.2)/5=18`
`3).`
Ta có: `ST \bot PQ` và `RP \bot PQ`
`=>ST //// RP`
Có: `QR=QS+SR=5+3,5=8,5`
`(QT)/(QP)=(QS)/(QR)`
`=>4/y=5/(8,5)`
`=>y=(4.8,5)/5`
`=>y=6,8`
`@Nae`