Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quãng đường người đó đi được sau n lần kéo là: \(100.{\left( {1 - 0,25} \right)^n}\)
Quãng đường người đó đi được sau 10 lần kéo là: \(100.{\left( {1 - 0,25} \right)^{10}} \approx 5,63\,\,\left( m \right)\)

Chọn D
Gọi r i là khoảng cách lần rơi thứ i
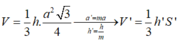
Ta có
![]()
Suy ra tổng các khoảng cách rơi của quả bóng từ lúc thả bóng cho đến lần rơi thứ n bằng 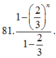
Gọi t i là khoảng cách lần nảy thứ i
Ta có
![]()
Suy ra tổng các khoảng cách nảy của quả bóng từ lúc thả bóng cho đến đến lần nảy thứ n bằng 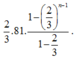
Vậy tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy nữa bằng
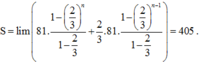

Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao của lần rơi ngay trước đó và sau đó lại rơi xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
- Thời điểm chạm đất lần thứ nhất là d 1 = 63
- Thời điểm chạm đất lần thứ hai là:
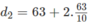
- Thời điểm chạm đất lần thứ ba là:
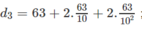
- Thời điểm chạm đất lần thứ tư là:
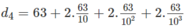
....
- Thời điểm chạm đất lần thứ n (n > 1) là
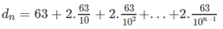
(Có thể chứng minh khẳng định này bằng quy nạp).
Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến khi nằm yên trên mặt đất là :
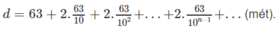
Vì 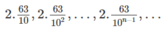
là một cấp số nhân lùi vô hạn, công bội q = 1/10 nên ta có
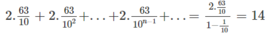
Vậy
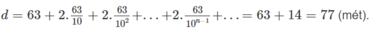

Gọi (un) là dãy số thể hiện quãng đường di chuyển của quả bóng sau mỗi lần chạm đất.
Ta có: \({u_1} = 55,8;{u_2} = \frac{1}{{10}}.{u_1};{u_3} = {\left( {\frac{1}{{10}}} \right)^2}.{u_1};...;{u_n} = {\left( {\frac{1}{{10}}} \right)^{n - 1}}.{u_1}.\)
Khi đó dãy (un) lập thành một cấp số nhân lùi vô hạn có số hạng đầu u1 = 55,8 và công bội \(q = \frac{1}{{10}}\) thỏa mãn \(\left| q \right| < 1.\)
\( \Rightarrow {S_n} = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{55,8}}{{1 - \frac{1}{{10}}}} = 62\left( m \right)\)
Vậy tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất n lần là 62 m.

Ta nhận xét rằng khi thả bóng thì bóng đi được 1 lược còn kể từ lần nảy đầu tiên đến khi dừng lại thì bóng đi được 2 lược (1 nảy lên và 1 rơi xuống). Giả sử sau lần nảy thứ n + 1 thì bóng dừng hẳn.
Quãng đường bóng đi được tính đến lần chạm sàn thứ nhất là:
\(S_1=63\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ 2 là:
\(S_2=63+63.\dfrac{1^1}{10^1}\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ (n + 1) là:
\(S_{n+1}=63+63.\left(\dfrac{1}{10}+\dfrac{1}{10^2}+...+\dfrac{1}{10^n}\right)\)
\(=63+63.\dfrac{\dfrac{1}{10}}{1-\dfrac{1}{10}}=70\left(m\right)\)
Vậy độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất là \(70\left(m\right)\)

Đáp án B
Bình có 2 khả năng thắng cuộc:
+) Thắng cuộc sau lần quay thứ nhất. Nếu Bình quay vào một trong 5 nấc: 80, 85, 90, 95, 100 thì sẽ thắng nên xác suất thắng cuộc của Bình trường hợp này là P 1 = 5 20 = 1 4
+) Thắng cuộc sau 2 lần quay. Nếu Bình quay lần 1 vào một trong 15 nấc: 5, 10, ..., 75 thì sẽ phải quay thêm lần thứ 2. Ứng với mỗi nấc quay trong lần thứ nhất, Bình cũng có 5 nấc để thắng cuộc trong lần quay thứ 2, vì thế xác suất thắng cuộc của Bình trường hợp này là P 2 = 15 × 5 20 × 20 = 3 16
Từ đó, xác suất thắng cuộc của Bình là
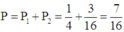




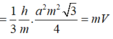
a, Độ cao nảy ngược lên của người đó là một cấp số nhân có số hạng đầu \(u_1=9\) và công bội \(q=60\%=0,6\)
Độ cao nảy ngược lên của người đó ở lần nảy thứ ba là:
\(u_3=u_1\cdot q^2=9\cdot\left(0,6\right)^2=3,24\left(m\right)\)
b, Tổng các độ cao nảy ngược lên của người đó trong 5 lần này đầu là:
\(S_5=\dfrac{u_1\left(1-q^5\right)}{1-q}=\dfrac{9\cdot\left(1-0,6^2\right)}{1-0,6}=20,7504\left(m\right)\)