Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

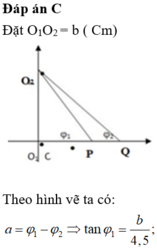
Đáp án C
+ Khoảng cách gần nhất giữa hai điểm cực đại trên đoạn S1S2 là 0,5λ = 1cm → λ = 2cm
→ Số cực đại giao thoa - S 1 S 2 λ ≤ k ≤ S 1 S 2 λ
⇔ - 4 , 75 ≤ k ≤ 4 , 75 → có 9 dãy
+ Mỗi dãy cực đại cắt đường tròn tại 2 điểm → có 18 điểm cực đại trên đường tròn.

Đáp án A.
Lời giải chi tiết:
Độ lệch pha của điểm M với hai nguồn là 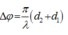
Điều kiện để M lệch pha π 2 so với nguồn:
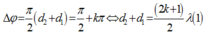
Vậy quỹ tích các điểm lệch pha π 2 so với nguồn là đường elip thỏa mãn đều kiện (1) nhận S1 và S2 làm tiêu điểm.
+ Điều kiện để các đường elip này nằm trong (E) là:
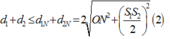
+ Mặt khác tổng các cạnh trong một tam giác lớn hơn cạnh còn lại nên
![]()
Kết hợp (1), (2) và (3) ta có:
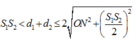
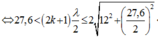

Vậy có 2 đường elip nằm trong € mà các điểm trên đó lệch pha π 2 so với nguồn.
+ Số điểm giao động với biên độ cực đại trên đoạn thẳng nối hai nguồn:
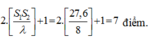
+ Vì 1 đường cực đại cắt elip tại 2 điểm nên trên 1 đường elip có 14 điểm dao động với biên độ cực đại.
Vậy trên 2 đường elip có 28 điểm dao động với biên độ cực đại và lệch pha π 2 số với nguồn.

Chọn đáp án B
? Lời giải:
+ Xét Δ M S 1 S 2
có M S 1 = 16cm; M S 2 = 25cm
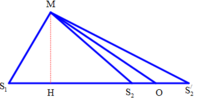


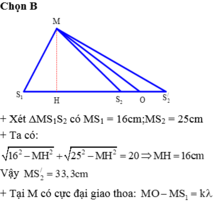
+ Vì O nằm trên khoảng S 2 S 2 '
M S 2 - M S 1 < k λ < M S 2 ' - M S 1 ⇒ 25 - 16 < 3 k < 33 , 3 - 16 ⇒ 3 < k < 5 , 7
Có hai giá trị k nguyên ứng với hai lần nguồn tạo ra tại M dao động với biên độ cực đại

Đáp án: C
HD Giải: 
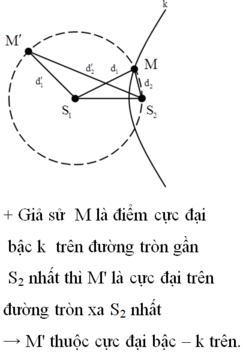
M gần S2 nhất nên M nằm trên đường cực đại số 6
Ta có MA - MB = 6λ
=> MB = MA - 6λ
= 10 - 6.1,5 = 1cm = 10mm