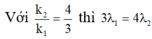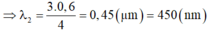Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

o 1,2 1,2,3 x T
Khoảng cách giữa 2 vân gần nhất có màu giống vân trung tâm là \(x_{\equiv}\)
\(\Rightarrow x_{\equiv}=k_1i_1=k_2i_2=k_3i_3\)\(\Rightarrow k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)(1)
Ta có: \(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{5}{4}\)
Vì trong khoảng giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm chỉ có một vị trí trùng nhau của các vân sáng ứng với hai bức xạ λ1, λ2 nên: \(\begin{cases}k_1=5.2=10\\k_2=4.2=8\end{cases}\)
Thay vào (1) ta có: \(10\lambda_1=8\lambda_2=k_3\lambda_3\)
λ3 có màu đỏ nên λ1 > λ2
\(\Rightarrow k_3<8\)
\(\Rightarrow k_3=7;5;3\)
+ \(k_3=7\Rightarrow\lambda_3=\frac{8}{7}\lambda_2=\frac{8}{7}.0,5=0,57\)
+ \(k_3=5\Rightarrow\lambda_3=\frac{8}{5}\lambda_2=\frac{8}{5}.0,5=0,8\)loại, vì ngoài bức xạ màu đỏ.
Vậy \(\lambda_3=0,57\mu m\), không có đáp án nào thỏa mãn :))
Ý này của bạn bị nhầm λ3 có màu đỏ nên λ1 > λ2
Sửa lại là: Vì \(\lambda_3\) có màu đỏ nên \(\lambda_3>\lambda_2\)

Chọn A
Ta có:
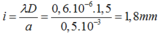
Tại điểm M trên màn cách vân sáng trung tâm (chính giữa) một khoảng 5,4 mm có vân sáng bậc :
x = ki => k = x/i = 5,4 /1,8 = 3



Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là
![]() =16
=16

Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)

Bạn tham khảo một bài hoàn toàn tương tự như vậy nhé
Câu hỏi của trần thị phương thảo - Học và thi online với HOC24