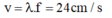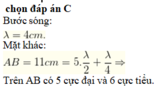Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda=\frac{v}{f}=\frac{12}{5}=2.4cm\)
Số điểm cực đại trong đoạn MN chính là số giá trị k thỏa mãn \(NO_{2}-NO_{1} \leq d_{2}-d_{1} \leq MO_{2}-MO_{1} \Rightarrow -12 \leq (k+ \frac{\triangle \phi}{2\pi})\lambda \leq 7\\ \Rightarrow -5.25 \leq k \leq 2.7 \)
=> k = -5,-4,-3,-2,-1,0,1,2. Có 8 vân cực đại trong đoạn MN.
Số điểm cực tiểu trong đoạn MN:
\(NO_{2}-NO_{1} \leq d_{2}-d_{1} \leq MO_{2}-MO_{1} \Rightarrow -12 \leq (2k+1+ \frac{\triangle \phi}{\pi})\frac{\lambda}{2} \leq 7\\ \Rightarrow -5.75\leq k \leq 2.16\)
=>k = -5,...,0,1,2. Có 8 vân cực tiểu trong đoạn MN.

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

Đáp án: D
HD Giải: λ = 50 10 = 5cm, d2 - d1 = 7,5 = 15λ suy ra tại M là cực tiểu số 2

Hai nguồn kết hợp A và B dao động với tần số f = 15 Hz và cùng pha
Tại M: d1 = 16cm và d2 = 20cm, sóng có biên độ cực tiểu.
Giữa M và đường trung trực của AB có 2 dãy cực đại nên M nằm trên cực tiểu thứ 3 nên d 2 - d 1 = 2 , 5 λ ⇒ λ = 1 , 6 c m Tốc độ truyền sóng trên mặt nước: v = λ . f = 24 c m / s
Chọn đáp án A

Đáp án A
Hai nguồn kết hợp A và B dao động với tần số f = 15 Hz và cùng pha
Tại M: d1=16 cm và d2=20 cm, sóng có biên độ cực tiểu.
Giữa M và đường trung trực của AB có 2 dãy cực đại
⇒ M nằm trên cực tiểu thứ 3 nên
![]()
suy ra Tốc độ truyền sóng trên mặt nước:
![]()

- Hai nguồn kết hợp A và B dao động với tần số f = 15 Hz và cùng pha
- Tại M: d1 = 16cm và d2 = 20cm, sóng có biên độ cực tiểu.
- Giữa M và đường trung trực của AB có 2 dãy cực đại nên M nằm trên cực tiểu thứ 3 nên:
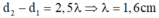
⇒ Tốc độ truyền sóng trên mặt nước: