Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải:
Ban đầu: 0,7 = ∆ k D a
Sau khi dịch chuyển màn: 0,84 = ∆ k ( D + 0 , 4 ) a
Trừ hai phương trình cho nhau ta được:
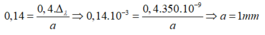
Đáp án C

Bề rộng quang phổ liên tục bậc 3 là
\(L = x_{đỏ}^k-x_{ tím}^k= 3\frac{D}{a}(\lambda_d-\lambda_t)=2,85mm.\)
Với \(D = 2m; a= 0,8mm; \lambda_d = 0,76 \mu m; \lambda_t = 0,38 \mu m.\)

Khoảng vân tím và khoảng vân đỏ :
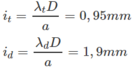
Bề rộng của quang phổ liên tục bậc 1 :
L 1 = i đ - i t = 1,9 - 0,95 = 0,95 mm Bề rộng của quang phổ liên tục bậc 3 :
L 3 = 3 i đ - 3 i t = 3.1,9 - 3.0,95 = 2,85 mm

Bề rộng quang phổ bậc 2: ∆i2 = 2D(λt – λd)/a
→a = 2D(λt – λd)/ ∆i2 = 0,96 mm
Chọn đáp án B



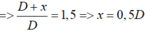
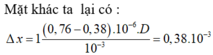
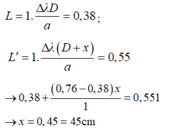
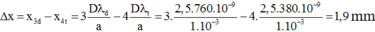
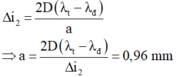
Đáp án C
Ban đầu:
Sau khi dịch chuyển màn:
Trừ hai phương trình cho nhau ta được: