Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
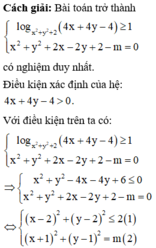
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
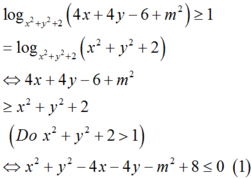
Ta có
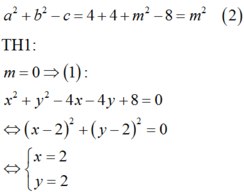
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
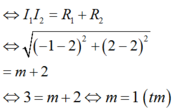
TH2: C1; C2 tiếp xúc trong và
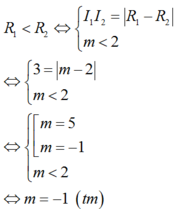
Vậy S = - 1 ; 1 .
Chọn D.
Đáp án A
Ta có e 2 x + y + 1 - e 3 x + 2 y = x + y + 1 ⇔ e 2 x + y + 1 + 2 x + y + 1 = e 3 x + 2 y + 3 x + 2 y *
Xét f t = e t + t là hàm số đồng biến trên ℝ mà f 2 x + y + 1 = f 3 x + 2 y ⇒ y = 1 - x
Khi đó log 2 2 2 x + y - 1 - m + 4 log 2 x + m 2 + 4 = 0
Phương trình (1) có nghiệm khi và chỉ khi ∆ = m + 4 - 4 m 2 + 4 ≥ 0 ⇔ 0 ≤ m ≤ 8 3 .
Ta có 
đồ thị hàm số luôn có TCN y = 1
Do đó để ycbt thỏa mãn 
Chọn C.
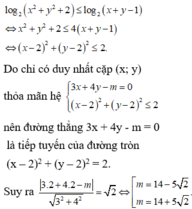
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9