Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

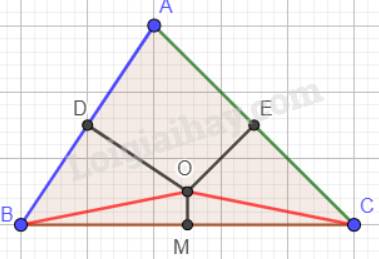
a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O. Suy ra: \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). ( tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
OB = OC;
\(\widehat {OBM} = \widehat {OCM}\);
MB = MC (M là trung điểm của đoạn thẳng BC).
Vậy \(\Delta OMB = \Delta OMC\)(c.g.c)
Do đó,\(\widehat {MOB} = \widehat {MOC}\) ( 2 góc tương ứng).

Vì AC là đường trung trực của BB' nên CB=CB'
=>ΔCBB' cân tại C
hay \(\widehat{BCA}=\widehat{B'CA}\)
Vì AB là đường trung trực của CC' nên BC=BC'
=>ΔBCC' cân tại B
hay \(\widehat{CBA}=\widehat{C'BA}\)
Vì AB và AC lần lượt là các đường phân giác của các góc CBB' và BCB'
và AB cắt AC tại A
nên A là điểm cách đều ba cạnh của ΔA'BC

giúp mình với nhé mai mình thi cuối học kì I môn toán rồi. Chúc các bạn có một kì thi tốt đẹp.
đề bài sai à
câu a tam giác vuông tại A mà góc B = 90o suy ra góc C = 0o à

+) Xét tam giác ADE và BDE có:
DE chung
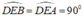
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
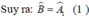
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
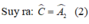
Từ (1) và (2) suy ra: 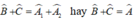

Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
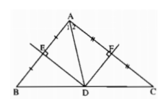
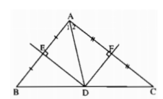

a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b)
Ta có ∆DEB = ∆DEA(c.g.c) nên ˆB=ˆA1B^=A1^. Tương tự ˆC=ˆA2C^=A2^.
Suy ra ˆA=ˆA1+ˆA2=ˆB+ˆC