Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M. N, P và Q theo thứ tự là trung điểm các cạnh AB, CD, BC và DA của tứ giác lồi ABCD
Khi đó :
\(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{BC}\right)\) và \(\overrightarrow{PQ}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{CD}\right)\)
Ta có : \(\left|\overrightarrow{MN}\right|+\left|\overrightarrow{PQ}\right|=\frac{1}{2}\left(\left|\overrightarrow{AD}+\overrightarrow{BC}\right|+\left|\overrightarrow{BA}+\overrightarrow{CD}\right|\right)\)
\(\le\frac{1}{2}\left(\left|\overrightarrow{AD}\right|+\left|\overrightarrow{BC}\right|+\left|\overrightarrow{BA}\right|+\left|\overrightarrow{CD}\right|\right)\)
Dấu đẳng thức xảy ra khi và chỉ khi \(\overrightarrow{AD}\uparrow\uparrow\overrightarrow{BC}\) và \(\overrightarrow{BA}\uparrow\uparrow\overrightarrow{CD}\)
Suy ra điều cần chứng minh

Để chứng minh rằng một đa giác lồi có n cạnh, khi được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3, ta có thể sử dụng phương pháp quy nạp (induction) để giải quyết bài toán này.
Đầu tiên, chúng ta xét trường hợp đơn giản nhất khi n = 3, tức là đa giác là tam giác. Trong trường hợp này, không cần vẽ đường chéo nào cả, vì tam giác đã được chia thành các tam giác bằng nhau. Và n = 3 chia hết cho 3.
Giả sử đa giác có n cạnh thỏa mãn điều kiện trong đề bài. Ta sẽ chứng minh rằng khi thêm một cạnh mới vào đa giác, tức là n+1 cạnh, thì n+1 cũng phải chia hết cho 3.
Giả sử đa giác có n cạnh và đã được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau. Khi thêm một cạnh mới vào đa giác, chúng ta sẽ thêm một tam giác mới và tạo ra một đường chéo mới. Khi đó, số tam giác trong đa giác tăng thêm một đơn vị và số đường chéo tăng thêm một đơn vị.
Điều quan trọng là ta phải đảm bảo rằng khi thêm một cạnh mới vào, chúng ta vẫn có thể chia đa giác thành các tam giác bằng nhau bằng cách vẽ n-2 đường chéo đôi một không cắt nhau. Điều này có nghĩa là ta cần thêm một đường chéo mới để duy trì tính chất của đa giác ban đầu.
Với việc thêm một cạnh mới, số đường chéo tăng lên một đơn vị, nên ta cần có (n-2)+1 = n-1 đường chéo. Điều này đồng nghĩa với việc n-1 phải chia hết cho 3.
Dựa trên quy nạp, chúng ta có thể kết luận rằng với mọi số tự nhiên n ≥ 3, nếu đa giác có n cạnh và được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3.
Vậy, điều phải chứng minh đã được chứng minh.

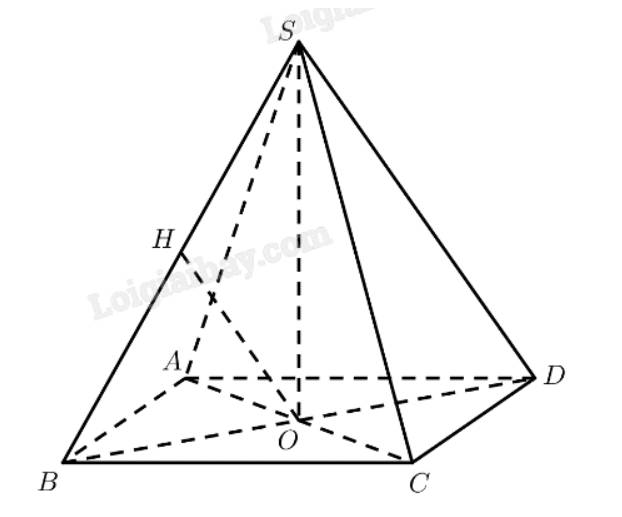
a) Kẻ \(OH \bot SB\left( {H \in SB} \right)\)
\(S.ABC{\rm{D}}\) là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot SB\)
\( \Rightarrow d\left( {AC,SB} \right) = OH\)
\(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông cân tại \(O\) có đường cao \(OH\)
\( \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}\)
b) \({S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\)