Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a bằng số dư của phép chia N cho 2 .
=> a = 1
=> abcd có dạng 1bcd.
e thuộc số dư của phép chia N cho 6.
=> e thuộc 0,1,2,3,4,5 mà d bằng số dư của phép chia N cho 5 .
=> d,e thuộc 00,11,22,33,44,05.
c thuộc số dư của phép chia N cho 4.
=> c,d,e thuộc 000,311,222,133,044,105.
=> a,b,c,d,e có dạng là 1b000,1b311,1b222,1b333,1b044,1b105.
Vì b bằng số dư của phép chia N cho 3
=> a+c+d+e chia hết cho 3 .
=> Chọn được số 1b311,1b044.
Ta được các số là : 10311,11311,12311,10044,11044,12044.
![]()

Các kết quả trên đều đúng cả nên mình điền luôn vào ô trống nha:
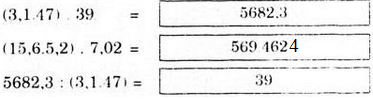
(3,1.47).39=5682,3.
(15,6.5,2).7,02=569,4624.
5682,3:(3,1.47)=39.
Đó là kết quả của mình nếu có gì sai thì bạn góp ý để mình sửa chữa nhé bạn!
- Các phép nhân đều cho kết quả đúng.
- Ta có:
(3,1 . 47) . 39 = 3,1 .(47 . 39) (tính chất kết hợp)
= 3,1 .1833 (theo a)
= 5682,3 (theo c)
(15,6 . 5,2) . 7,02 = (15,6 . 7,02) . 5,2 (Tính chất giao hoán và kết hợp)
= 109,512 . 5,2 (theo b)
= 569,4624 (theo d)
5682,3 : (3,1 . 47) = (5682,3 : 3,1) : 47
= 1833 : 47 (suy từ c) = 39 (suy từ a)
Vì vậy ta có thể điền các số thích hợp vào ô trống mà không cần tính toán.

a: A là tập hợp các số tự nhiên chẵn có 2 chữ số
=>A={10;12;14;...;98}
Số phần tử của tập hợp A là:
\(\frac{98-10}{2}+1=\frac{88}{2}+1=44+1=45\) (phần tử)
b: B là tập hợp các số tự nhiên chẵn có 2 chữ số
=>B={10;12;14;...;98}
Số phần tử của tập hợp B là:
\(\frac{98-10}{2}+1=\frac{88}{2}+1=44+1=45\) (phần tử)
c: C là tập hợp các số tự nhiên lẻ có 3 chữ số
=>C={101;103;...;999}
Số phần tử của tập hợp C là:
\(\left(999-101\right):2+1=898:2+1=449+1=450\) (phần tử)