Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Theo định luật bảo toàn số khối ta có X có khối lượng 6u
Vì hạt α bay ra có phương vuông góc với p ban đầu, áp dụng định luật bảo toàn động lượng cho ta
P X 2 = P α 2 + P P 2 ; mà ta cũng có p 2 = 2 m K nên m X K X = m α K α + m P K P ⇒ K X = 3 , 575
Từ định luật bảo toàn năng lượng toàn phần và định nghĩa năng lượng tỏa ra ta có năng lượng tỏa ra
W t = K X + K α − K P = 3 , 575 + 4 − 5 , 45 = 2 , 125 M e V

Đáp án A
+ Vì hạt a bay ra vuông góc với hạt p ban đầu nên: ![]() Û
2
m
X
K
X
=
2
m
α
K
α
+
2
m
p
K
p
Û
2
m
X
K
X
=
2
m
α
K
α
+
2
m
p
K
p
+ Áp dụng bảo toàn số khối ta được số khối của X: A X = 1 + 9 - 4 = 6
®
12
K
X
=
8
K
α
+
2
K
p
® ![]() MeV
MeV
+ DE = K X + K α - 2 K p = 3,575 + 4 - 5,45 = 2,125 MeV.

Đáp án A
Phương pháp: Sử dụng định luật bảo toàn động lượng.
Cách giải: Ta có thể biểu diễn các vecto động lượng như hình vẽ:
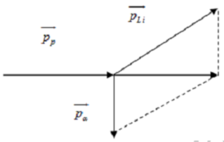
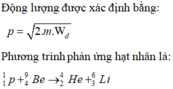
Áp dụng định luật bảo toàn động lượng cho hệ hai hạt p và Be.
![]()
Gọi góc giữa vec to động lượng của Li và vecto tổng động lượng là α. Ta có
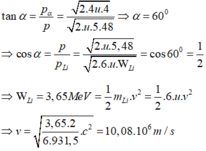

Đáp án B
Theo đề, sau n chuỗi phản ứng công suất của lò chỉ còn 34% với hệ số nhân notron là 0,95 nên:
![]()
- số phản ứng đã xảy ra:
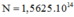
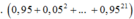
![]()
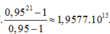
- Năng lượng tỏa ra từ các phân hạch trong thời gian lò giảm công suất là:
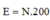
![]()

Đáp án A
Phương trình phản ứng là:
![]()
Gọi ∆E là năng lượng tỏa ra của phản ứng, ta có:
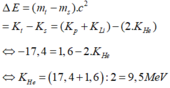

Đáp án D
Đối với dạng toán phản ứng hạt nhân, không kèm theo bức xạ γ ta đi đến phương pháp tổng quát.
Hạt A (đạn) bắn vào hạt B đứng yên (bia) sinh ra hai hạt C và D thì áp dụng định luật bảo toàn động lượng:
![]()
Định luật bảo toàn và chuyển hóa năng lượng:
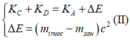
Xét bài toán đã cho. Áp dụng định luật bảo toàn năng lượng:
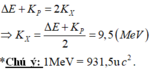



Đáp án C