Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:![]()
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì ![]() là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho ![]() là:
là:
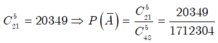
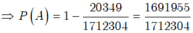

Xét 2 biến cố:
D: “Bạn Hương được chọn song ca” => P(D) = 0,9
E: “Bạn Dũng được chọn song ca” => P(E) = 0,7
a) Do \(A = D \cap E \Rightarrow P(A) = P(D).P(E) = 0,7.0,9 = 0,63\)
b) Ta thấy \(B = E \cup D \Rightarrow P(B) = P(E \cup D) = P(E) + P(D) - P(E \cap D) = 0,7 + 0,9 - 0,63 = 0,97\)
c) Xét biến cố đối \(\overline D \) của biến cố D. Ta thấy \(P\left( {\overline D } \right) = 1 - P(D) = 1 - 0,9 = 0,1\)
Vì \(C = E \cap \overline D \Rightarrow P(C) = P(E).P\left( {\overline D } \right) = 0,1.0,7 = 0,07\)

Số cách xếp 9 học sinh là 9!
Xếp 2 học sinh lớp 10 đứng cạnh nhau có 2!=2 cách
n(omega)=9!
TH1: 2 học sinh lớp 10 cạnh nhau
=>2*8!
TH2: 2 học sinh lớp 10 đứng xen kẽ với học sinh lớp 12
=>Có 2*4*7! cách
TH3: 2 học sinh lớp 12 đứng giữa hai học sinh lớp 10
=>Có \(2\cdot A^2_4\cdot6!\left(cách\right)\)
TH4: 3 học sinh lớp 12 đứng giữa hai học sinh lớp 10
=>Có \(2\cdot A^3_4\cdot5!\left(cách\right)\)
TH5: 4 học sinh lớp 12 đứng giữa hai học sinh lớp 10
=>Có \(2\cdot A^4_4\cdot4!\left(cách\right)\)
=>n(A)=145152
=>P(A)=2/5

Ta đi tìm số cách chọn ra 5 bạn mà trong đó có cả hai bạn Thùy và Thiện.
Bước 1: Chọn nhóm 3 em trong 13 em, trừ Thùy và Thiện thì có ![]() cách.
cách.
Bước 2: Ghép 2 em Thùy và Thiện có 1 cách.
Vậy theo quy tắc nhân thì có 286 cách chọn 5 em trong đó cả Thùy hoặc Thiện đều được chọn.
- Chọn 5 em bất kì trong số 15 em có ![]() cách. Vậy theo yêu cầu đề bài thì có tất cả 3003-286=2717 cách chọn mà trong đó có ít nhất một trong hai em Thùy và Thiện không được chọn.
cách. Vậy theo yêu cầu đề bài thì có tất cả 3003-286=2717 cách chọn mà trong đó có ít nhất một trong hai em Thùy và Thiện không được chọn.
Chọn C.

Chọn D
Vì mỗi học sinh lớp 12A được đăng kí 1 hoặc 2 tiết mục trong số 3 tiết mục văn nghệ nên số cách lựa chọn tiết mục văn nghệ của mỗi học sinh là: C 3 1 + C 3 2 = 6.
Lớp 12A có 44 học sinh đều tham gia văn nghệ nên số cách để lớp lựa chọn là: 6 44 .

Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 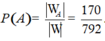
Chọn C.

Đáp án A
+) Chọn 3 tiết mục bất kì có C 9 3 = 84 (cách).
+) Chọn 1 tiết mục của khối 10 có 3 cách. Chọn tiếp 1 tiết mục của khối 11 không trùng với nội dung đã chọn của khối 11 có 2 cách. Chọn tiếp 1 tiết mục của khối 12 không trùng với nội dung đã chọn của khối 10 và khối 11 có 1 cách. Do đó cá 6 cách chọn các tiết mục thoản mãn yêu cầu đề bài.
Vậy xác suất cần tính là 6 84 = 1 14

Đáp án A
Chọn 3 tiết mục bất kỳ có: Ω = C 9 3 = 84 cách.
Gọi A là biến cố: “ba tiết mục được chọn có đủ cả ba khối và đủ cả ba nội dung”.
Khối 10 chọn 1 tiết mục có 3 cách
khối 11 chọn 1 tiết mục khác khối 10 có 2 cách
tương tự khối 12 có 1 cách
Ta có: Ω A = 3 . 2 . 1 = 6 cách
Vậy P = 6 84 = 1 14

Đáp án A
Có 2 trường hợp như sau
+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2 = 210 cách chọn
+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1 = 35 cách chọn
Suy ra xác suất cần tính bằng
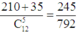
Chọn A
Ghi nhớ: Công thức cộng xác suất: