Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Đường tròn (C) có tâm O(1;–2). T u → ( O ) = O ' . Áp dụng biểu thức tọa độ ta có: x ' − 1 = − 1 y ' + 2 = 3
<=> x ' = 0 y ' = 1 Đường tròn tâm O’(0;1) bán kính 3
Phương trình đường tròn cần tìm: x 2 + y − 1 2 = 3

Đáp án B
Q ( O ; 180 o ) : I → I ' (–1;1) , bán kính 3
T u → ( I ) = I ' 1 ; − 2 bán kính 3
Phương trình đường tròn (C”): x − 1 2 + y + 2 2 = 9

Đáp án C
Q ( O ; 180 o ) : I → I ' (0;1) , bán kính 3
I ' ' = V O ; k ( I ' ) => I”(0;2), bán kính 6
T u → ( I " ) = I ' " 1 ; 4 , bán kính 6
Phương trình đường tròn (C”): ( x − 1 ) 2 + y − 4 2 = 36

Đáp án A
(C) có I( 1; –3), bán kính R = 2
Áp dụng biểu thức tọa độ x ' = x + a y ' = y + b , ta có I’ (–1;0)=>(C’): ( x + 1 ) 2 + y 2 = 4

Đáp án C
(C) có tâm I(0;2), bán kính 5
Tịnh tiến theo vectơ u → biến I thành I’(2; 0)
=>Phương trình đường tròn (C’): ( x − 2 ) 2 + y 2 = 25

a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
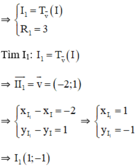
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒ 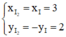 ⇒ I2(3; 2)
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒ 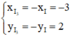
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.


Đáp án B
T u → ( I ) = I ' − 2 ; − 6 , bán kính 3