Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
Xác suất đội A thắng mỗi hiệp là 0,4 (không có hòa) nên xác suất đội A thua mỗi hiệp là 0,6.
Gọi X là biến cố đội A thắng trận đấu với đội B.
Gọi X1, X2, X3 tương ứng là biến cố đội A thắng đội B với tỉ số lần lượt là 3-0; 3-1; 3-2.
Khi đó X = X 1 ∪ X 2 ∪ X 3 và X1, X2, X3 đôi một xung khắc.
Ta có P(X) = P( X 1 ∪ X 2 ∪ X 3 ) = P(X1) + P(X2) + P(X3).
Xét biến cố X1: Đội A thắng đội B với tỉ số 3-0.
Khi đó phải đấu 3 hiệp và đội A thắng cả 3 hiệp ⇒ P X 1 = 0 , 4 3 = 8 125
Xét biến cố X2: Đội A thắng đội B với tỉ số 3-1.
Khi đó phải đấu 4 hiệp và đội B thắng duy nhất 1 trong 3 hiệp đầu
⇒ P X 2 = C 3 1 . 0 , 6 . 0 , 4 2 . 0 , 4 = 72 625
Xét biến cố X3: Đội A thắng đội B với tỉ số 3-2.
Khi đó phải đấu 5 hiệp và đội B thắng 2 trong 4 hiệp đầu, đội A thắng 3 hiệp còn lại
⇒ P X 3 = C 4 2 . 0 , 6 2 . 0 , 4 2 . 0 , 4 = 432 3125
Vậy xác suất để đội A thắng trận chung kết trên là:
P X = 8 125 + 72 625 + 432 3125 = 992 3125 = 0 , 31744 ≈ 0 , 317

Chọn C.
Phương pháp:
Cách giải: Để người thứ nhất thắng thì hoặc người thứ nhất thắng 1 ván hoặc người thứ 2 thắng ít hơn 3 ván.
Vậy xác suất để người chơi thứ nhất giành chiến thắng là
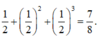

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Ta có :
\(K=\frac{2\sqrt{x}+3}{\sqrt{x}-5}=\frac{2\sqrt{x}-10}{\sqrt{x}-5}+\frac{13}{\sqrt{x}-5}=2+\frac{13}{\sqrt{x}-5}\)là số nguyên dương
<=> 13 chia hết cho \(\sqrt{x}-5\)
<=> \(\sqrt{x}-5\inƯ\left(13\right)=\left\{-13;-1;1;13\right\}\)
<=> \(\sqrt{x}\in\left\{-12;4;6;18\right\}\)
<=> \(x\in\left\{16;36;324\right\}\) (vì \(\sqrt{x}\ge0\))
Do x nguyên và x có GTLN nên x = 324


Đáp án là A