Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi D là khoảng cách từ màn mang hai khe F 1 , F 2 đến mặt phẳng tiêu vật của kính lúp, ở vị trí thứ nhất, và D + 30 là khoảng cách ở vị trí thứ hai. Ta có hai phương trình :
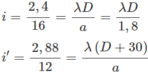
Giải ra ta được : D = 50 cm và λ = 0,54 μm.

Chọn C
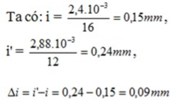
Khi dời màn ra xa thêm 0,3m thì khoảng vân tăng thêm 0,09mm thêm tức là :
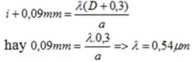

Gọi L là khoảng cách giữa hai vân sáng ngoài cùng
N là số vân sang quan sát được
Ta có hai trường hợp :
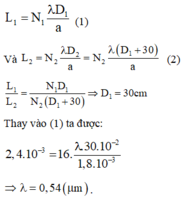
Đáp án B

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

Số vân sáng trong khoảng giữa hai vân sáng nằm ở hai đầu là
\(N_s = 2[\frac{L}{2i}]+1=> \frac{L}{2i }= 10=> i = 2mm.\)
\(\lambda = \frac{ai}{D}= 0,6 \mu m.\)

Khoảng cách giữa 7 vân sáng liên tiếp là
\((7-1)i = 2,4mm=> i = 0,4mm.\)
\(\lambda = \frac{ia}{D}=\frac{0,4.2}{1,2}=0,67\mu m. \)

\(i = \frac{\lambda D}{a} = 2mm.\)
Số vân tối quan sát trên màn là
\(N_t = 2.[\frac{L}{2i}+0,5]=16.\)

Tại vị trí cách vân trung tâm 3 mm có vân sáng bậc \(k\) của bức xạ \(\lambda\) khi
\(x=3mm = ki =k\frac{\lambda D}{a}.\)
=> \(\lambda = \frac{3.a}{D k}.(1)\)
Mặt khác : \(0,38 \mu m \leq \lambda \leq 0,76 \mu m.\)
<=> \(0,38 \mu m \leq \frac{3a}{kD} \leq 0,76 \mu m.\)
<=> \(\frac{3.0,8}{0,76.2} \leq k \leq \frac{3.0,8}{0,38.2} \)
Giữ nguyên đơn vị của \(x = 3mm; a = 0,8mm;\lambda = 0,76 \mu m;0,38 \mu m; D= 2m\)
<=> \(1,57 \leq k \leq 3,15.\)
<=> \(k = 2,3.\)
Thay vào (1) ta thu được hai bước sóng là \(\lambda_1 = \frac{3.0,8}{2.2}=0,6\mu m.\)
\(\lambda_2 = \frac{3.0,8}{3.2}=0,4\mu m.\)
Kính lúp đóng vai trò chính là màn hứng.
Lúc đầu: \(i = \frac{\lambda D}{a}= \frac{2,4}{16}= 0,15mm.(1)\)
\(i' = \frac{\lambda (D+0,3)}{a}= 0,24mm.\)
=> \(\frac{i}{i'}= \frac{D}{D+0,3}= \frac{5}{8}.\)
=> \(D = 0,5m.\)
Bước sóng của bức xạ là \(\lambda = \frac{ai}{D} = \frac{1,8.0,15}{0,5}=0,54 \mu m.\)
em lại cứ tưởng cái kính lúp đáng sợ lắm