Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
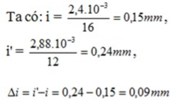
Khi dời màn ra xa thêm 0,3m thì khoảng vân tăng thêm 0,09mm thêm tức là :
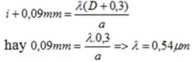

Gọi L là khoảng cách giữa hai vân sáng ngoài cùng
N là số vân sang quan sát được
Ta có hai trường hợp :
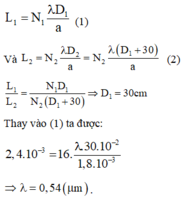
Đáp án B

Kính lúp đóng vai trò chính là màn hứng.
Lúc đầu: \(i = \frac{\lambda D}{a}= \frac{2,4}{16}= 0,15mm.(1)\)
\(i' = \frac{\lambda (D+0,3)}{a}= 0,24mm.\)
=> \(\frac{i}{i'}= \frac{D}{D+0,3}= \frac{5}{8}.\)
=> \(D = 0,5m.\)
Bước sóng của bức xạ là \(\lambda = \frac{ai}{D} = \frac{1,8.0,15}{0,5}=0,54 \mu m.\)

Khi quan sát vân bằng kính lúp thì ta trông thấy ảnh của hệ vân nằm trên mặt phẳng tiêu vật của kính lúp và ảnh đó ở xa vô cùng (H.25.1G).
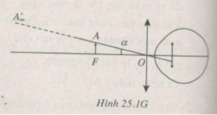
Ta thấy α = tan α = i/f = 12,5'
Khoảng cách từ hai khe tới mặt phẳng của các vân : D = L - f = 40 - 4 = 36 cm = 0,36 m.
Bước sóng của bức xạ là :
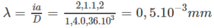

Trong môi trường chiết suất n, tốc độ ánh sáng giảm n lần nhưng tần số không đổi, do đó bước sóng và khoảng vân i giảm n lần.
Ta có:
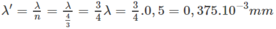
và khoảng cách giữa hai vân nói trên thành 1,575 mm

Khi quan sát bằng kính lúp thì ta trông thấy ảnh của hệ vân nằm trên một mặt phẳng gọi là tiêu diện của kính lúp và khi đó ảnh ở xa vô cực
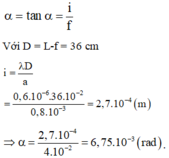
Đáp án C

Với λ 0 , ta có i 0 = 3,3/(8 - 1) = 3,3/7 mm
Với λ ta có i = 3,37/(9 - 1) = 3,37/8 mm
Do đó ta có
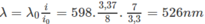

Chọn A.
Trong khoảng từ vân sáng thứ 4 đến vân sáng thứ 10 có 6 khoảng vân i, suy ra i = 0,4mm. Bước sóng ánh sáng được tính theo công thức λD/A. Suy ra λ = 0,40 µm.
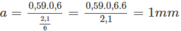
Gọi D là khoảng cách từ màn mang hai khe F 1 , F 2 đến mặt phẳng tiêu vật của kính lúp, ở vị trí thứ nhất, và D + 30 là khoảng cách ở vị trí thứ hai. Ta có hai phương trình :
Giải ra ta được : D = 50 cm và λ = 0,54 μm.