

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
+ Bước sóng của sóng λ = 2 πv ω = 4 cm .
Số cực đại trên đoạn thẳng nối hai nguồn:
- AB λ ≤ k ≤ A B λ ⇔ - 2 , 5 ≤ k ≤ 2 , 5 .
+ Để trên đoạn AM không còn cực đại nào khác thì M là cực đại ứng với k = 2.
+ Ta có
BM - AM = 8 BM 2 - AM 2 = AB 2 ⇒ ( 8 + AM 2 ) - AM 2 = 10 2 ⇒ AM = 2 , 25 cm .

Đáp án D
+ Bước sóng: λ = v/f = 40/20 = 20(cm)
+ Vì hai nguồn ngược pha và điểm M thuộc cực đại nên: MA – MB = (k + 0,5)λ
+ Điểm M gần A nhất khi M thuộc đường cực đại gần A nhất.
+ Số cực đại trên AB:
- AB λ - 1 2 < k < AB λ - 1 2
=> - 8,5 < k < 7,5 => điểm M thuộc k = - 8
=> MA – MB = -15 => MB = MA + 15 (1)
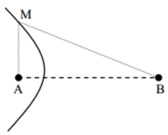
+ Trong tam giác vuông AMB ta có:
MB2 = MA2 + AB2 , từ (1) ta có (MA + 15)2 = MA2 + 162 => MA ≈ 1,033 cm .

Đáp án D
+ Bước sóng: ![]()
+ Vì hai nguồn ngược pha và điểm M thuộc cực đại nên: MA – MB = (k + 0,5)λ
+ Điểm M gần A nhất khi M thuộc đường cực đại gần A nhất.
+ Số cực đại trên AB: ![]()
=> - 8,5 < k < 7,5 => điểm M thuộc k = - 8
=> MA – MB = -15 => MB = MA + 15 (1)
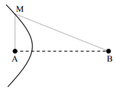
+ Trong tam giác vuông AMB ta có:
MB2 = MA2 + AB2,
từ (1) ta có (MA + 15)2 = MA2 + 162
=> MA ≈ 1,033 cm.

Đáp án D
+ Bước sóng: λ = v f = 40 20 = 2 c m
+ Vì hai nguồn ngược pha nên điều kiện cực đại cho M là: M A − M B = k + 0 , 5 λ = 2 k + 1
+ Vì M gần A nhất nên M phải thuộc cực đại ngoài cùng về phía A.
+ Số cực đại trên AB: − A B λ − 1 2 < k < A B λ − 1 2
⇒ − 8 , 5 < k < 8 , 5 ⇒ k = − 8
⇒ M A − M B = 2 − 8 + 1 = − 15 ⇒ M B = M A + 15 1
+ Vì Δ A M B vuông tại A nên: M A 2 + A B 2 = M B 2 2
+ Thay (1) vào (2) ta có: M A 2 + 16 2 = M A + 15 2 ⇒ M A = 1 , 03 c m
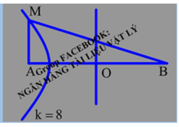

Chọn A

trên đoạn AB có 5 “bó sóng” vớ O là bụng của bó trung tâm. Các bó đối xứng nhau qua một bụng thì cùng pha nên có hai điểm khác cùng pha với O

Số điểm cực đại trên đoạn AG là số giá trị k thỏa mãn \(-AG \leq (k+\frac{\triangle \phi}{2\pi})\lambda \leq AG \Rightarrow -\frac{AB}{4}.3=10.875cm \leq (k+0.5)\lambda \leq 10.875\\ \Rightarrow -5.94 \leq k \leq 4.94 \Rightarrow k = -5,-4,\ldots,0,1,\ldots,4\)
có 10 điểm dao động cực đại trên đoạn AG

+ Gọi d1, d2 là khoảng cách từ M đến 2 nguồn ( M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông → d12 + d22 = ( 8 2 ) 2
+ M dao động với biên độ cực đại nên: d1 - d2 = kl
Mà λ = v . T = 0 , 6 . 2 π 30 π = 0 , 04 m m
+ Giải hệ phương trình trên ta được: 2d22 + 8kd2 + 16k2 - 128 = 0
Chỉ có k = 0 là thỏa mãn → d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên d1 + d2 = 2k’l → k’ = 2
Vậy có tất cả 2 điểm.
Đáp án D