Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi A là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.
B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.
⇒ A C = a 3 A ∪ B là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.
A ∩ B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.
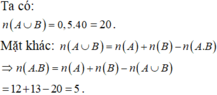

a) Xác suất để có 2 sinh viên thi đậu:
\(0,6.0,7.0,2+0,6.0,3.0,8+0,4.0,7.0,8=0,452\)
b) Xác suất để có 2 sinh viên thi đậu trong đó sinh viên II không thi đậu:
\(0,6.0,3.0,8=0,144\)

Kí hiệu A 1 , A 2 , A 3 lần lượt là các biến cố: Học sinh được chọn từ khối I trượt Toán, Lí, Hoá: B 1 , B 2 , B 3 lần lượt là các biến cố : Học sinh được chọn từ khối II trượt Toán, Lí, Hoá. Rõ ràng với mọi (i,j), các biến cố A i và B i độc lập.
a) 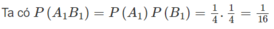
b) Xác suất cần tính là
P ( ( A 1 ∪ A 2 ∪ A 2 ) ∩ ( B 1 ∪ B 2 ∪ B 3 ) ) = P ( A 1 ∪ A 2 ∪ A 2 ) . P ( B 1 ∪ B 2 ∪ B 3 ) = 1 / 2 . 1 / 2 = 1 / 4
c) Đặt A = A 1 ∪ A 2 ∪ A 3 , B = B 1 ∪ B 2 ∪ B 3
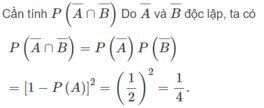
d) Cần tính P(A ∪ B)
Ta có
P(A ∪ B) = P(A) + P(B) − P(AB)
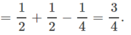

Đáp án D
Để thi đậu thí sinh có thể vượt qua kì thi ở một trong 3 vòng.
Xác suất thí sinh đậu vòng 1 là p1 = 0,9
Xác suất thí sinh đậu vòng 2 là p2 = 0,1.0,7 = 0,07
Xác suất thí sinh đậu vòng 3 là p3 = 0,1.0,3.0,3 = 0,009
Vậy xác suất thí sinh đậu kì thi là: p = p1 + p2 + p3 = 0,9 + 0,07 + 0,009 = 0,979

Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách
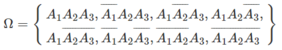
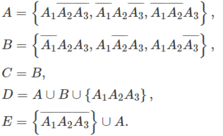

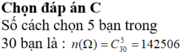
Gọi \(B_1\) là biến cố "sinh viên A đạt môn thứ nhất"
\(B_2\) là biến cố "sinh viên A đạt môn thứ hai"
\(\Rightarrow P\left(B_1\right)=0,8\) ; \(P\left(B_2|B_1\right)=0,6\) ; \(P\left(B_2|\overline{B_1}\right)=0,3\)
a/ Xác suất đạt môn thứ hai:
\(P\left(B_2\right)=P\left(B_1\right).P\left(B_2|B_1\right)+P\left(\overline{B_1}\right)P\left(B_2|\overline{B_1}\right)\)
\(=0,8.0,6+0,2.0,3=0,54\)
b/ Xác suất để đạt ít nhất 1 môn:
\(P\left(B_1\cup B_2\right)=P\left(B_1\right)+P\left(B_2\right)-P\left(B_1B_2\right)\)
\(=P\left(B_1\right)+P\left(B_2\right)-P\left(B_1\right)P\left(B_2|B_1\right)=0,86\)