Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp này giống với bảng A World Cup năm nay, đội A là Mexico, đội B là Brazil, đội C là Croatia và đội D là Cameroon.
Trước lượt trận cuối cùng, đội B là Brazil và đội A là Mexico sau trận hoà có cùng 4 điểm, đội D là Cameroon không có điểm nào cả, đội B cần phải thắng để có thể ít nhất là đi tiếp.
Trường hợp đội A và đội B đều hoà thì chắc chắn đội C bị loại.
Trường hợp đội A thắng đội C thì đương nhiên. Trường hợp đội A thua đội C và đội B thua đội D thì đội C sẽ đi tiếp với 6 điểm (nhất bảng), đội A và B phải xét hiệu số bàn thắng thua.", là lời giải của thành viên Nam Mốc.
Còn thành viên Minh Tĩnh thì suy đoán: "D 0đ suy ra A 4đ, vậy B cũng 4đ, C 3đ. Nếu B thua D và A thua C thì B 4đ, A 4đ, D 3đ và C 6đ nên vẫn có khả năng C nhất bảng."
Trong khi đó, thành viên Hiếu Trung Nguyễn đưa ra một lời giải khá tỉ mỉ: "Em tính như sau ạ:
Lượt 1:
A hòa B (theo giả thiết)
C thắng D (Do D chưa thắng trận nào)
Lượt 2
A thắng D (Do D chưa thắng trận nào)
B thắng C (Do A đã được thắng 1, hòa 1. Mặt khác A và B bằng điểm (theo giả thiết)
Vậy hết lượt 2:
A và B cùng 4 điểm
C 3 điểm
D 0 điểm
Lượt 3:
Nếu A thua C ---> A 4 điểm, C 6 điểm
Nếu B thua D ---> B 4 điểm, D 3 điểm
---> C đứng đầu bảng mà không phụ thuộc hiệu số."
Với cách lập luận ngắn gọn, logic thành viên Nvan Acons đã đưa ra lời giải chính xác: "Từ giả thiết đội D muốn thắng để có 3 điểm, chứng tỏ đội D trước đó gặp A và C toàn thua, B và A bằng điểm mà A đã thắng D và hòa B nên cục diện bảng này là A và B cùng có 4 điểm, C có 3 điểm, D chưa có điểm, nếu C thắng A và B không thắng D thì C sẽ đầu bảng với 6 điểm.

Vì tổng số trận đấu là 10 trận khi đó \(\frac{x(x-1)}{2}=10\)
Ta có : \(\frac{x(x-1)}{2}=10\)
\(\Rightarrow x(x-1)=10\cdot2\)
\(\Rightarrow x(x-1)=20\)
Do 20 = 4.5 nên có 5 đội tham gia thi đấu

a) Ta tính tổng số các cặp lớp phân biệt có thể xảy ra.
Vị trí đầu tiên có \(x\) cách chọn và vị trí thứ hai sẽ có \(x-1\) cách chọn (do một lớp bất kì không thể đấu với chính lớp đó). Nhưng nếu tính như trên, thì mỗi trận đấu giữa 2 đội bất kì sẽ bị lặp lại thêm 1 lần, nên tổng số trận đấu khác nhau là \(\dfrac{x\left(x-1\right)}{2}\)
b) Cho \(\dfrac{x\left(x-1\right)}{2}=105\)
\(\Leftrightarrow x^2-x-210=0\)
\(\Leftrightarrow\left(x-21\right)\left(x+20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=21\left(nhận\right)\\x=-20\left(loại\right)\end{matrix}\right.\)
Vậy có 21 đội tham gia.

Gọi x là số câu trả lời đúng
Số câu trả lời sai: 10 – x
Sau khi trả lời 10 câu thì người dự thi sẽ có: 5x – (10 – x) + 10
Để được dự thi tiếp vòng sau thì
5x – (10 – x ) +10 ≥ 40
⇔ 5x - 10 + x + 10 ≥ 40
⇔6x ≥ 40
⇔ x ≥\(\dfrac{20}{3}\) Vì x là số nguyên dương nhỏ hơn hay bằng 10 nên 203≤x≤10203≤x≤10
Vậy người dự thi phải trả lời chính xác ít nhất 7 câu hỏi thì mới được dự thi tiếp ở vòng sau.

Gọi x là số câu hỏi được trả lời đúng ở vòng sơ tuyển (x nguyên dương)
Số câu hỏi trả lời sai: 10 – x
Số điểm người dự thi đạt được: 10 + 5x – (10 -x)
Người dự thi muốn thi tiếp vòng sau thì 10 + 5x – (10 -x) ≥ 40
⇔ 6x ≥ 40 ⇔ x ≥ 20/3. Do x nguyên dương nên x ∈ {7;8;9;10}

Gọi x là số câu trả lời đúng (0 ≤ x ≤ 10, x ∈ N)
Số câu trả lời sai: 10 – x
Trả lời đúng x câu được 5x (điểm), trả lời sai 10 –x (câu) bị trừ (10- x) điểm.
Do đó, sau khi trả lời 10 câu thì người dự thi sẽ có: 5x – (10 – x) + 10
Để được dự thi tiếp vòng sau thì
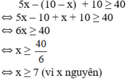
Vậy người dự thi phải trả lời chính xác ít nhất 7 câu hỏi thì mới được dự thi ở vòng sau.


JUF98WE