Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:

Gọi A : “bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí”
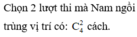
Trong 2 lượt đó, lượt đầu: Nam có 24 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại; lượt sau: Nam có 1 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại.
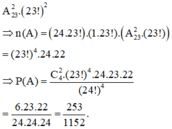

Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu : n Ω = 24 4
A: “Bình và Lan có chung đúng một mã đề thi”
- Chọn một môn chung mã đề thi có : 2 cách
- Chọn một mã chung có: 24 cách
- Chọn mã môn còn lại:
+) Cho Bình: 24 cách
+) Cho Lan: 23 cách
Xác suất:
P A = n A n Ω = 2.24.24.23 24 4 = 23 288

Chọn C.
Hai bạn Bình và Lan cùng 1 mã đề, cùng 1 môn thi (Toán hoặc TA) có 24 cách.
Môn còn lại khác nhau ⇒ có 24.23 cách chọn.
Do đó, có 2.24.24.23 = 26496 cách để Bình, Lan có chung mã đề.
Vậy xác suất cần tính là P = 26496 24 2 . 24 2 = 23 288 .

Đáp án B
The đề bài ta có C n − 2 2 C n 4 = 2 C n − 2 4 C n 4 ⇔ n = 7 .

Chọn C

Gọi A là biến cố để Hùng và Hương chỉ có chung đúng một môn tự chọn và một mã đề thi. Các cặp gồm 2 môn thi tự chọn mà mỗi cặp có đúng một môn thi là 3 cặp, gồm:
Cặp thứ nhất (Vật lý, Hóa học) và (Vật lý, Sinh học)
Cặp thứ hai ( Hóa học,Vật lý) và (Hóa học, Sinh học)
Cặp thứ ba (Sinh học, Hóa học) và (Sinh học,Vật lý)



Đáp án D
Để thi đậu thí sinh có thể vượt qua kì thi ở một trong 3 vòng.
Xác suất thí sinh đậu vòng 1 là: p 1 = 0 , 9
Xác suất thí sinh đậu vòng 2 là: p 2 = 0 , 1.0 , 7 = 0 , 07
Xác suất thí sinh đậu vòng 3 là: p 3 = 0 , 1.0 , 3 , 0 , 3 = 0 , 009
Vậy xác suất thí sinh đậu kì thi là:
p = p 1 + p 2 + p 3 = 0 , 9 + 0 , 07 + 0 , 009 = 0 , 979