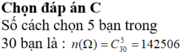Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Số phần tử của không gian mẫu là số các số 4 chữ số lập từ các số 0; 1; 2; 3; 4; 5; 6 là ![]()
- Số cách chọn một số có hàng đơn vị là số 0 có ![]() cách
cách
- Số cách chọn một số có hàng đơn vị là số 5 có ![]() cách
cách
- Suy ra số cách chọn một số chia hết cho 5 là ![]() cách
cách
Vậy xác suất cần tìm bằng ![]() .
.

Trong không gian mẫu \(\Omega\) là tập hợp gồm tất cả các cặp hai bộ 3 câu hỏi, mà ở vị trí thứ nhất của cặp là bộ 3 câu hỏi thí sinh A chọn và ở vị trí thứ hai của cặp là bộ 3 câu hỏi thí sinh B chọn
Vì A cũng như B đều có \(C_{10}^3\) cách chọn 3 câu hỏi tứ 10 câu hỏi thí sinh nên theo quy tắc nhân ta có \(n\left(\Omega\right)=\left(C_{10}^3\right)^2\)
Kí hiệu X là biến cố " bộ 3 câu hỏi A chọn và bộ 3 câu hỏi B chọn là giống nhau"
Vì mỗi cách chọn 3 câu hỏi của A, B chỉ có duy nhất cách chọn 3 câu hỏi giống như A nên \(n\left(\Omega_X\right)=C_{10}^3.1=C_{10}^3\)
Vì vậy \(P\left(X\right)=\frac{n\left(\Omega_X\right)}{n\left(\Omega\right)}=\frac{C^3_{10}}{\left(C^3_{10}\right)^2}=\frac{1}{C^3_{10}}=\frac{1}{120}\)

Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi
có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 + 210 = 3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323

Đáp án A
Lấy ngẫu nhiên từ ngân hàng đề thi 4 câu hỏi để lập một đề thi có C 20 4 = 4845 đề thi.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 2 câu đã thuộc
có C 10 2 . C 10 2 = 2025 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 3 câu đã thuộc
có C 10 3 . C 10 1 = 1200 trường hợp.
Thí sinh A rút ngẫu nhiên được 1 đề thi có 4 câu đã thuộc
có C 10 4 = 210 trường hợp.
Do đó, thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc
có 2025 + 1200 +210 =3435 trường hợp.
Vậy xác suất để thí sinh A rút ngẫu nhiên được 1 đề thi có ít nhất 2 câu đã thuộc là
3435 4845 = 229 323

Đáp án D
Để thi đậu thí sinh có thể vượt qua kì thi ở một trong 3 vòng.
Xác suất thí sinh đậu vòng 1 là p1 = 0,9
Xác suất thí sinh đậu vòng 2 là p2 = 0,1.0,7 = 0,07
Xác suất thí sinh đậu vòng 3 là p3 = 0,1.0,3.0,3 = 0,009
Vậy xác suất thí sinh đậu kì thi là: p = p1 + p2 + p3 = 0,9 + 0,07 + 0,009 = 0,979

Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách