Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x,y lần lựợt là số lít nước cam và nước táo cần pha chế.
Số điểm thưởng nhận được là F = 60x + 80y.
Ta có hệ BPT 30 x + 10 y ≤ 210 x + y ≤ 9 x + 4 y ≤ 24 x ≥ 0 ; y ≥ 0 . Miền nghiệm của hệ như hình vẽ.
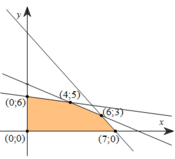
Giá trị lớn nhất của F đạt được tại điểm (4;5). Vậy đội A đã pha chế 4 lít nước cam và 5 lít nước táo.
Đáp án D.

Chọn đáp án C
Phương pháp
- Lập hệ bất phương trình ẩn x, y dựa vào điều kiện đề bài.
- Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ.
- Tìm x, y để biểu thức tính số điểm M(x;y) đạt GTLN (tại một trong các điểm mút).
Cách giải
Gọi x, y lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế (x≥0;y≥0)
Để pha chế x lít nước cam thì cần 30x (g) đường, x lít nước và x (g) hương liệu.
Để pha chế y lít nước táo thì cần 10y (g) đường, y lít nước và 4y (g) hương liệu.
Theo bài ra ta có hệ bất phương trình:
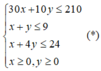
Số điểm đạt được khi pha x lít nước cam và y lít nước táo là: M(x;y)=60x+80y.
Bài toán trở thành tìm x, t thỏa để M(x;y) đạt GTLN.
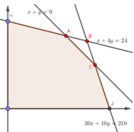
Ta biểu diễn miền nghiệm của (*) trên mặt phẳng tọa độ như sau:
Miền nghiệm là ngũ giác ACJIH
Tọa độ các giao điểm A(4;5),C(6;3),J(7;0),I(0;0),H(0;6).
M(x;y) sẽ đạt max, min tại các điểm đầu mút nên thay tọa độ từng giao điểm vào tính M(x;y) ta được:
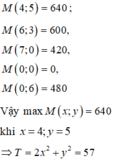

Bài 1 : Giải
Lượng đường trong 1,2kg nước ngọt là: 1,2 x 5 : 100 = 0,06kg
Để có tỉ lệ đường 2,5% thì lượng nước đường là: 0,06 x 100 : 2,5 = 2,4kg
Vậy lượng nước lọc cần đổ thêm là : 2,4 – 1,2 = 1,2 kg
ĐS : 1,2kg
Bài 2 : Giải
Lượng muối trong 1,2kg nước muối là: 1,2 x 3 : 100 = 0,036kg
Để có tỉ lệ muối 2,5% thì lượng nước muối là: 0,036 x 100 : 2,5 = 1,44kg
Vậy lượng nước lọc cần đổ thêm là : 1,44 – 1,2 = 0,24 kg
ĐS : 0,24kg

tính thời gian bể chảy dổi 1.36 ra dm chia cho số phút lá xong

số phần bể chảy là:
1/3+1/5=8/15
số phần bể có ban đầu là:
1-8/15=7/15
số phần trăm nước có sẵn tromg bể chiếm bể nước là
(7 : 15) x 100=46.7%
vậy số nước chiếm trong bể là 46.7 phần trăm
giữ lời hứa đó

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
Chọn C.
Gọi số lít nước ngọt loại I là x và số lít nước ngọt loại II là y. Khi đó ta có hệ điều kiện về vật liệu ban đầu mà mỗi loại được cung cấp: